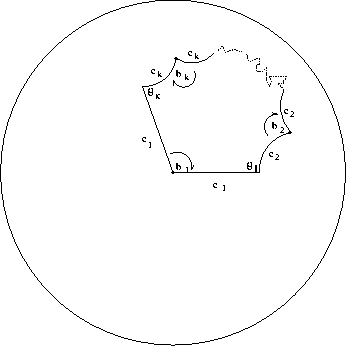
Figure: Fundamental polygon of theorem
To find the fundamental polygon we use the following theorem

Figure: Fundamental polygon of theorem ![]()
 be integers greater or equal than two
and let
be integers greater or equal than two
and let  be an integer greater than two, excepting the case
when
be an integer greater than two, excepting the case
when  is three and all
is three and all 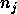 are equal to two. Then for each
are equal to two. Then for each
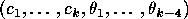 in an open set in
in an open set in
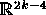 (if
(if 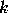 is greater than three;
is greater than three; 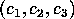 if
if 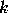 is three),
there exists a hyperbolic polygon (see figure
is three),
there exists a hyperbolic polygon (see figure 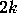 consecutive sides of lengths
consecutive sides of lengths
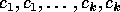 and respective interior angles
and respective interior angles
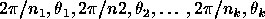 ,
where
,
where 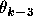 (if
(if 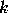 is greater than three),
is greater than three),
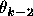 ,
, 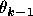 and
and 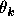 are uniquely determined and satisfy
are uniquely determined and satisfy

Moreover, for any such polygon, the group 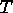 generated by the
elliptic elements
generated by the
elliptic elements 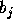 which pair consecutive sides of lengths
which pair consecutive sides of lengths
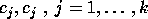 , is a Fuchsian group with the
given fundamental polygon; furthermore,
, is a Fuchsian group with the
given fundamental polygon; furthermore, 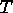 uniformizes
uniformizes 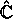 with signature
with signature
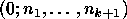 and has a presentation of the form
and has a presentation of the form
Proof: See [GR93].
Still following [GR93] we define define a homomorphism

by extension of 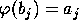 , for
, for 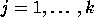 ;
then
;
then 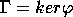 is a torsion-free Fuchsian group;
in fact, it is the smallest normal subgroup of
is a torsion-free Fuchsian group;
in fact, it is the smallest normal subgroup of 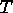 generated by
the words
generated by
the words 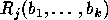 .
Also,
.
Also, 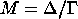 is a compact Riemann surfaces of
genus
is a compact Riemann surfaces of
genus 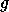 , and the natural projection from
, and the natural projection from
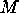 to
to 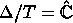 is a Galois covering with the prescribed
signature and covering group
is a Galois covering with the prescribed
signature and covering group 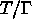 which is isomorphic to
which is isomorphic to
 .
.
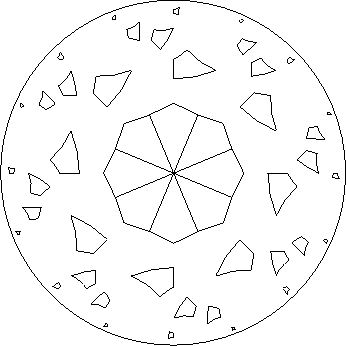
Figure: Polygon drawn using DFS labeling
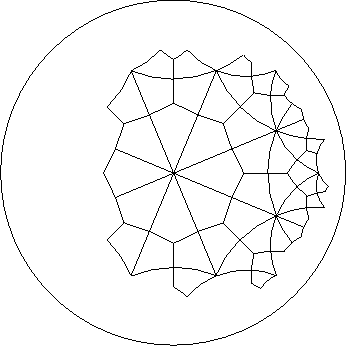
Figure: Polygon drawn using BFS labeling
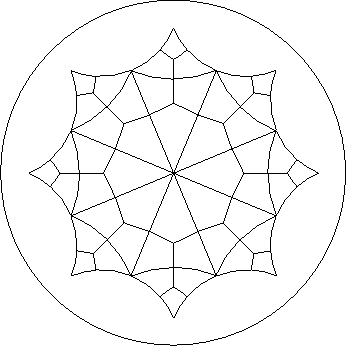
Figure: Polygon drawn using ``symmetric'' BFS labeling
So we want to construct the fundamental region  for
for  ,
taking
,
taking  images of
images of  under elements of
under elements of 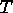 .
To choose this images we label each element in
.
To choose this images we label each element in  with a word on
the generators and then use that word to construct an element in
with a word on
the generators and then use that word to construct an element in
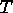 ,
standard techniques,
such as breadth first search (BFS) or depth first search (DFS),
produce strange labelings that leaded to unconnected or
non-symmetrical polygons,
see for example figures
,
standard techniques,
such as breadth first search (BFS) or depth first search (DFS),
produce strange labelings that leaded to unconnected or
non-symmetrical polygons,
see for example figures ![]() ,
, ![]() and
and
![]() ;
in all of them
;
in all of them  is
is
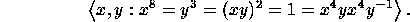
The best results are obtained using a modified version of BFS,
the idea is to maintain symmetry according to the first generator,
![]() let us call
let us call

the first generator; as in BFS a queue is used to keep the vertices that need processing, this queue is initialized with the identity vertex and those vertices where the user has already chosen a label (this is done to respect user preference, see below) then for each vertex

in the queue the vertices corresponding to

are labeled as

, where

is the label for

. Now each vertex

in the queue is processed as follows, unless already labeled a neighbour

of

across an edge coloured

is labeled

, where

is the label of

, and added to the queue (this is normal BFS), the vertices

are labeled

and added to the queue, unless they have been labeled already; the process continues until the queue is empty.
Sometimes the user may want a different labeling of the group, Unifpack provides methods to change some words and all labeling algorithms respect user preferences.
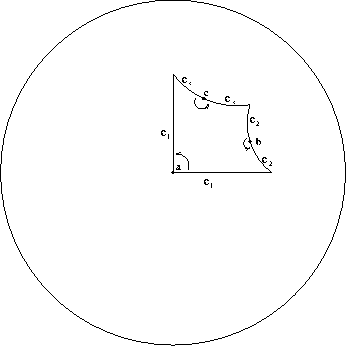
Figure: A fundamental polygon parametrized by side lengths
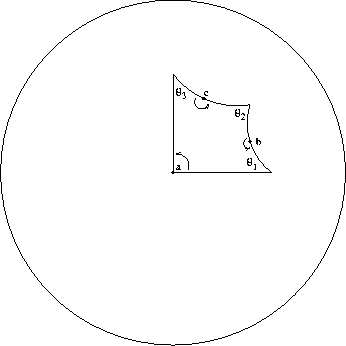
Figure: A fundamental polygon parametrized by angles
Sometimes a better set of parameters than the ones provided by
theorem ![]() can be found
(see figures
can be found
(see figures ![]() and
and ![]() ),
to exploit this possibility Unifpack defines polygon types,
when calculating the polygon from the group it tries to determine
the best polygon type for the group,
mechanisms are provided to add new (user defined) polygon types.
),
to exploit this possibility Unifpack defines polygon types,
when calculating the polygon from the group it tries to determine
the best polygon type for the group,
mechanisms are provided to add new (user defined) polygon types.
A polygon type also calculates initial or default values for the parameters it take, the fundamental region

the generators of the group

, checks if it can handle a presentation, provides methods to draw

and I/O functions.