Groups



Next: Polygons
Up: The algorithms
Previous: The algorithms
Mainly to fix notations and for the sake of completeness we recall here
some well know definitions and constructions that we will need.
Consider a group  ,
a subset
,
a subset 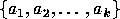 of
of
 is called a set of generators iff the smallest subgroup that
contains
is called a set of generators iff the smallest subgroup that
contains 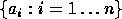 is all
is all  .
Given a set of generators a finite sequence of the symbols
.
Given a set of generators a finite sequence of the symbols
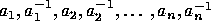 is called a word on the generators;
we say that the generators satisfy the relation
is called a word on the generators;
we say that the generators satisfy the relation 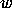 ,
where
,
where 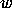 is a word on them,
if the element obtained multiplying the symbols of
is a word on them,
if the element obtained multiplying the symbols of 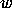 is the identity;
a word is said to be in reduced form if all the pairs of the form
is the identity;
a word is said to be in reduced form if all the pairs of the form
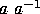 or
or 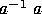 have been removed from it,
as this could left an empty word
we use the convention that the empty word is in reduced form
and call it the identity word, we usually represent it by
have been removed from it,
as this could left an empty word
we use the convention that the empty word is in reduced form
and call it the identity word, we usually represent it by 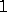 .
.
We would like to describe groups just naming their generators and
relations, but often, if not always this is just impossible, for
instance the Klein group is generated by two elements 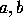 such that
such that
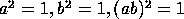 ,
but also the group of two elements
,
but also the group of two elements 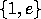 satisfies these properties with
satisfies these properties with 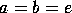 .
One could argue that what we want is the largest group that satisfy
those relations, but then the problem of the existence of such a group
arise.
Fortunately one can prove that there is always such a group,
we reproduce here the construction because it is interesting in what
follows.
.
One could argue that what we want is the largest group that satisfy
those relations, but then the problem of the existence of such a group
arise.
Fortunately one can prove that there is always such a group,
we reproduce here the construction because it is interesting in what
follows.
We first build a group that contains the generators
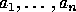 .
Consider the set of reduced words on the generators with the operation
of composition, it is easy to check that this is a group,
where the identity element is the empty word
(thus the name we gave it above),
and the inverse of a word
.
Consider the set of reduced words on the generators with the operation
of composition, it is easy to check that this is a group,
where the identity element is the empty word
(thus the name we gave it above),
and the inverse of a word
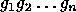 is the word
is the word
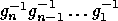 .
Notice that in fact the generators ``belong'' to this group,
each represented by the sequence
.
Notice that in fact the generators ``belong'' to this group,
each represented by the sequence 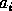 .
The group just built is called the free group on the generators,
we will write it as
.
The group just built is called the free group on the generators,
we will write it as 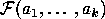 or simply
or simply 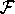 .
.
The given relations are members of 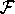 ,
so we can consider the smallest normal subgroup
,
so we can consider the smallest normal subgroup 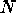 of
of 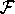 that contains all the relations,
and let us call
that contains all the relations,
and let us call  the quotient
the quotient 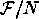 .
Now
.
Now  does satisfy the prescribed relations,
to prove that
does satisfy the prescribed relations,
to prove that  in the
largest possible group let
in the
largest possible group let 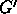 be a group
generated by a set
be a group
generated by a set 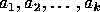 that satisfy the
relations,
then there is a natural function
that satisfy the
relations,
then there is a natural function

that maps each word 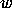 to the product of the symbols in
to the product of the symbols in 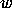 ,
it is easy to see that this map is an homomorphism of groups,
and that its kernel contains
,
it is easy to see that this map is an homomorphism of groups,
and that its kernel contains 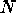 ,
because
,
because 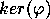 is a normal subgroup,
and since
is a normal subgroup,
and since 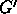 satisfy the relations they are mapped to the
identity in
satisfy the relations they are mapped to the
identity in 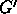 ,
so
,
so 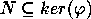 , from the isomorphism theorems follow
that
, from the isomorphism theorems follow
that  is an extension of
is an extension of 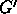 , so
, so  is the largest group
generated by
is the largest group
generated by 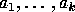 subject to the given restrictions.
subject to the given restrictions.
A group  is said to have presentation
is said to have presentation
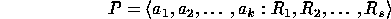
if  is isomorphic to the largest group generated by the elements
is isomorphic to the largest group generated by the elements
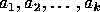 that satisfies the relations
that satisfies the relations 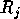 .
Of course the same group can have many presentations.
.
Of course the same group can have many presentations.
We now prove that it is possible to find the multiplication table of a
finite group given a presentation for it,
it is known that this is not possible for infinite groups,
but we do not address that problem here.
Consider a group  (possibly infinite) with a presentation
(possibly infinite) with a presentation
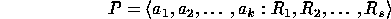
were 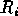 is a word in the generators
is a word in the generators 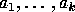 ,
we can associate a graph to the pair
,
we can associate a graph to the pair 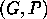 as follows,
the vertices of the graph are the elements of
as follows,
the vertices of the graph are the elements of  ,
we join two vertices
,
we join two vertices  and
and  by an edge
by an edge  if there is a
generator
if there is a
generator 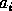 such that
such that 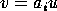 ,
we say that this edge has color
,
we say that this edge has color 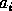 ,
notice that the edge is naturally oriented leaving
,
notice that the edge is naturally oriented leaving  and
arriving to
and
arriving to  ,
we add another oriented edge from
,
we add another oriented edge from  to
to  with color
with color 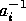 .
This graph
.
This graph 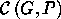 is called the Cayley graph of
is called the Cayley graph of  for the presentation
for the presentation 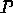 ,
notice that in fact the graph depends on the presentation,
to see this is enough to add a new generator to a given presentation,
then the new graph contains two more edges on each vertex.
,
notice that in fact the graph depends on the presentation,
to see this is enough to add a new generator to a given presentation,
then the new graph contains two more edges on each vertex.
Given a word 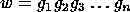 on the generators
on the generators
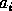 and a vertex
and a vertex  in
in 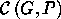 there is only one path
such that it starts on
there is only one path
such that it starts on  and its edges are colored
and its edges are colored
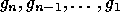 ,
conversely to each path we can associate
a word which we will call the name of the path.
Notice that if a path starts in the element
,
conversely to each path we can associate
a word which we will call the name of the path.
Notice that if a path starts in the element 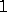 and has name
and has name 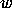 its
ending vertex is exactly the one associated to the element in
its
ending vertex is exactly the one associated to the element in  which
the word
which
the word 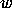 represents.
represents.
The Cayley graph can be used to find the multiplication
table of  ,
since the set
,
since the set 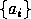 generates
generates  for each
element
for each
element  in
in  there is a word
there is a word 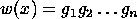 in the
generators such that
in the
generators such that 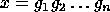 ,
this means that the path starting from
,
this means that the path starting from 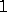 with name
with name 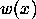 ends on the
vertex
ends on the
vertex  ,
notice also that the path starting from
,
notice also that the path starting from 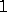 with name
with name 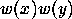 ends
on the element
ends
on the element 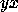 ,
thus we can find the product of
,
thus we can find the product of  and
and 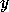 simply finding the ending
vertex of the path
simply finding the ending
vertex of the path 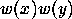 .
Even more the words
.
Even more the words 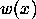 induce a labeling in the nodes, we can use
that labeling to recognize the elements and write the multiplication
table.
induce a labeling in the nodes, we can use
that labeling to recognize the elements and write the multiplication
table.
We also just proved that the Cayley graph is connected, because each
element is connected to the vertex 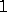 by the path with name
by the path with name 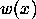 ,
it can be easily proved too that a path is a loop iff its name
represents the identity in
,
it can be easily proved too that a path is a loop iff its name
represents the identity in  .
.
In this way our original problem has been reduced to finding the Cayley
graph of the group,
although at first this doesn't look very promising
(since we don't even have the order of the group, that is we don't even
know how many vertices the graph has)
we will prove that the Cayley
graph really solves our problem.
We first observe that a Cayley graph 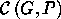 satisfies the following
properties
satisfies the following
properties
- It is not empty and connected.
The first assertion comes from the fact that
 is non empty, above we proved the second.
is non empty, above we proved the second.
-
On each vertex incides exactly one edge for each color.
-
If from vertex
 originates an edge of color
originates an edge of color  arriving to
vertex
arriving to
vertex  then from
then from  originates an edge of color
originates an edge of color 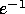 to
to  .
.
This last two properties come from the definition of 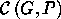
-
To each word
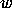 in the generators of
in the generators of  we can associate a
unique path
we can associate a
unique path 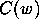 starting from the node
starting from the node 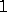 .
.
This comes from the previous properties.
-
A path
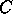 is a loop iff its name belong to
is a loop iff its name belong to 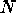 (the normal
subgroup defined above).
(the normal
subgroup defined above).
We noticed that a path is a loop iff its name is the identity in  ,
but then its name must belong to
,
but then its name must belong to 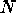 from the definition of
from the definition of 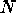 .
.
Suppose we have colored graph 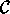 with vertex set
with vertex set
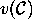 and colors
and colors
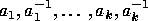 that satisfies the properties above,
we can define a function
that satisfies the properties above,
we can define a function
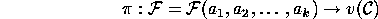
that maps each word 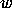 to the ending vertex of the path
to the ending vertex of the path 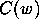 defined in property
defined in property  .
Consider the equivalence relation on
.
Consider the equivalence relation on 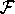 defined by
defined by
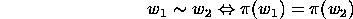
is clear that there is a bijection between 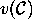 and
and
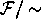 .
On the other hand if
.
On the other hand if
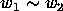 then
then
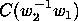 is a loop, but then
is a loop, but then
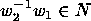 ,
so
,
so
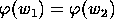 ,
where
,
where 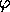 is the natural map
is the natural map

so 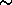 is exactly the equivalence relation in the quotient
is exactly the equivalence relation in the quotient
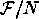 ,
then there is a
,
then there is a 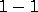 and onto map
and onto map

We want to extend 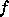 to a isomorphism of graphs between
to a isomorphism of graphs between 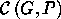 and
and
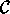 , in fact, two vertices
, in fact, two vertices 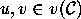 are joined
by an edge
are joined
by an edge  of color
of color  iff the ending vertex of
iff the ending vertex of 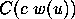 is the
vertex
is the
vertex  iff
iff 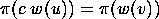 iff
iff
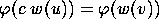 iff
iff
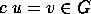 iff
iff
 is joined to
is joined to  by an edge of color
by an edge of color  .
.

Figure: An algorithm to calculate 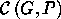
Let us now consider the algorithm in figure  ,
a vertex is called ``filled'' if has all the needed edges,
i.e. there is at least one edge of each color on it,
the algorithm ``fills'' a vertex adding all the needed edges,
since the destination of the edges are unknown at first an extra
vertex is added as destination,
,
a vertex is called ``filled'' if has all the needed edges,
i.e. there is at least one edge of each color on it,
the algorithm ``fills'' a vertex adding all the needed edges,
since the destination of the edges are unknown at first an extra
vertex is added as destination,
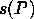 is the starting vertex of the path
is the starting vertex of the path 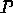 and
and 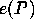 is the ending
vertex of it,
step (2.2.1) makes the path a loop,
this step may ``overfill'' the new (identified) vertex
because two or more edges of the same color may contain it,
this induces new identifications on the neighbors of the vertex
(to eliminate the extra edges),
this identifications must be propagated along the graph.
is the ending
vertex of it,
step (2.2.1) makes the path a loop,
this step may ``overfill'' the new (identified) vertex
because two or more edges of the same color may contain it,
this induces new identifications on the neighbors of the vertex
(to eliminate the extra edges),
this identifications must be propagated along the graph.
It is easy to see that if the algorithm stops then the graph obtained
satisfy the properties above, so it is isomorphic to 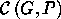 .
.
We will now prove that
that if  is finite the algorithm stops,
although this is quite intuitive a formal proof gives some insight.
is finite the algorithm stops,
although this is quite intuitive a formal proof gives some insight.
Let 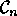 be the graph produced after
be the graph produced after 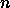 iterations before
entering the external loop (step (2)),
notice that in
iterations before
entering the external loop (step (2)),
notice that in 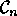 the path
the path 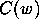 is well defined,
if
is well defined,
if 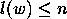 , where
, where 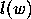 is the length of the word
is the length of the word 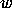 ;
for each
;
for each
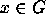 let
let 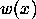 be the shortest word
(lexicographically minimal if there are several)
that satisfy
be the shortest word
(lexicographically minimal if there are several)
that satisfy 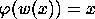 ,
then after at most
,
then after at most 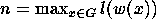 iterations the graph
iterations the graph 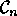 produced by the algorithm contains
at least one vertex for each element
produced by the algorithm contains
at least one vertex for each element 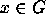 ,
namely
,
namely 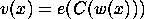 .
.
For any 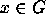 and
and 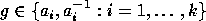 define
define 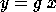 ,
we want to prove that after a finite number of iterations the vertices
,
we want to prove that after a finite number of iterations the vertices
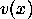 and
and 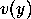 are joined by an edge of color
are joined by an edge of color 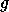 , we now that after
at most
, we now that after
at most 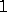 iteration
iteration 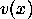 has all its edges in particular
has all its edges in particular  of
color
of
color 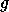 , if the destination of
, if the destination of 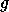 is
is 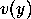 then there is nothing
to prove, otherwise let
then there is nothing
to prove, otherwise let  be the destination of
be the destination of  ,
then
,
then 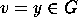 , but then there is a word
, but then there is a word 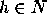 such that
such that
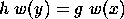 , but
, but

where 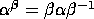 y
y
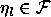 ,
but then after at most
,
but then after at most
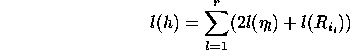
the step (2.2) of the algorithm warrants that  has been identified
with
has been identified
with 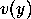 .
Since there is a finite number of pairs
.
Since there is a finite number of pairs 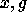 after a finite number of
iterations (
after a finite number of
iterations (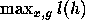 ) the graph
) the graph 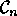 contains an
isomorphic copy of
contains an
isomorphic copy of 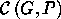 , namely the subgraph generated by the
vertices
, namely the subgraph generated by the
vertices 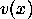 where
where 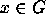 , but then those are all the vertices of
, but then those are all the vertices of
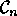 ,
if not so because the graph
is connected,
there must be one vertex
,
if not so because the graph
is connected,
there must be one vertex 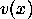 from where an
edge originates to an extra vertex
from where an
edge originates to an extra vertex  ,
but from the construction there
is only one edge for each color coming out of
,
but from the construction there
is only one edge for each color coming out of 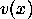 and all of them go
to the
and all of them go
to the 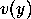 vertices, this is a contradiction.
At last notice that all the
vertices, this is a contradiction.
At last notice that all the 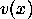 vertices are filled, so the
algorithm stops.
vertices are filled, so the
algorithm stops.



Next: Polygons
Up: The algorithms
Previous: The algorithms
coryan@mat.puc.cl
 ,
a subset
,
a subset 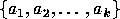 of
of
 is called a set of generators iff the smallest subgroup that
contains
is called a set of generators iff the smallest subgroup that
contains 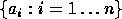 is all
is all  .
Given a set of generators a finite sequence of the symbols
.
Given a set of generators a finite sequence of the symbols
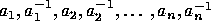 is called a word on the generators;
we say that the generators satisfy the relation
is called a word on the generators;
we say that the generators satisfy the relation 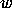 ,
where
,
where  is a word on them,
if the element obtained multiplying the symbols of
is a word on them,
if the element obtained multiplying the symbols of 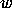 is the identity;
a word is said to be in reduced form if all the pairs of the form
is the identity;
a word is said to be in reduced form if all the pairs of the form
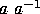 or
or 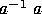 have been removed from it,
as this could left an empty word
we use the convention that the empty word is in reduced form
and call it the identity word, we usually represent it by
have been removed from it,
as this could left an empty word
we use the convention that the empty word is in reduced form
and call it the identity word, we usually represent it by 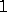 .
.
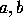 such that
such that
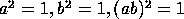 ,
but also the group of two elements
,
but also the group of two elements 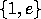 satisfies these properties with
satisfies these properties with 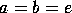 .
One could argue that what we want is the largest group that satisfy
those relations, but then the problem of the existence of such a group
arise.
Fortunately one can prove that there is always such a group,
we reproduce here the construction because it is interesting in what
follows.
.
One could argue that what we want is the largest group that satisfy
those relations, but then the problem of the existence of such a group
arise.
Fortunately one can prove that there is always such a group,
we reproduce here the construction because it is interesting in what
follows.
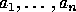 .
Consider the set of reduced words on the generators with the operation
of composition, it is easy to check that this is a group,
where the identity element is the empty word
(thus the name we gave it above),
and the inverse of a word
.
Consider the set of reduced words on the generators with the operation
of composition, it is easy to check that this is a group,
where the identity element is the empty word
(thus the name we gave it above),
and the inverse of a word
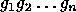 is the word
is the word
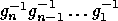 .
Notice that in fact the generators ``belong'' to this group,
each represented by the sequence
.
Notice that in fact the generators ``belong'' to this group,
each represented by the sequence 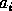 .
The group just built is called the free group on the generators,
we will write it as
.
The group just built is called the free group on the generators,
we will write it as 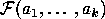 or simply
or simply 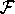 .
.
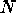 of
of 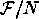 .
Now
.
Now 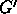 be a group
generated by a set
be a group
generated by a set 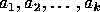 that satisfy the
relations,
then there is a natural function
that satisfy the
relations,
then there is a natural function 
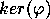 is a normal subgroup,
and since
is a normal subgroup,
and since 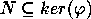 , from the isomorphism theorems follow
that
, from the isomorphism theorems follow
that 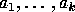 subject to the given restrictions.
subject to the given restrictions.
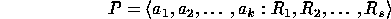
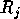 .
Of course the same group can have many presentations.
.
Of course the same group can have many presentations.
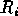 is a word in the generators
is a word in the generators 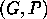 as follows,
the vertices of the graph are the elements of
as follows,
the vertices of the graph are the elements of  and
and  by an edge
by an edge  if there is a
generator
if there is a
generator 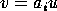 ,
we say that this edge has color
,
we say that this edge has color 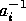 .
This graph
.
This graph 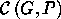 is called the Cayley graph of
is called the Cayley graph of 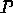 ,
notice that in fact the graph depends on the presentation,
to see this is enough to add a new generator to a given presentation,
then the new graph contains two more edges on each vertex.
,
notice that in fact the graph depends on the presentation,
to see this is enough to add a new generator to a given presentation,
then the new graph contains two more edges on each vertex.
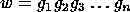 on the generators
on the generators
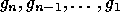 ,
conversely to each path we can associate
a word which we will call the name of the path.
Notice that if a path starts in the element
,
conversely to each path we can associate
a word which we will call the name of the path.
Notice that if a path starts in the element 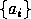 generates
generates  in
in 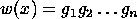 in the
generators such that
in the
generators such that 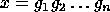 ,
this means that the path starting from
,
this means that the path starting from 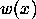 ends on the
vertex
ends on the
vertex 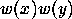 ends
on the element
ends
on the element 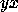 ,
thus we can find the product of
,
thus we can find the product of 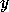 simply finding the ending
vertex of the path
simply finding the ending
vertex of the path 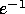 to
to 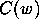 starting from the node
starting from the node 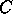 is a loop iff its name belong to
is a loop iff its name belong to 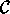 with vertex set
with vertex set
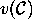 and colors
and colors
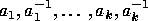 that satisfies the properties above,
we can define a function
that satisfies the properties above,
we can define a function 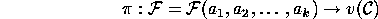
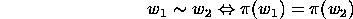
 .
On the other hand if
.
On the other hand if
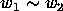 then
then
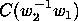 is a loop, but then
is a loop, but then
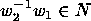 ,
so
,
so
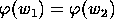 ,
where
,
where 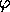 is the natural map
is the natural map
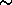 is exactly the equivalence relation in the quotient
is exactly the equivalence relation in the quotient
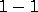 and onto map
and onto map 
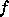 to a isomorphism of graphs between
to a isomorphism of graphs between 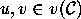 are joined
by an edge
are joined
by an edge  iff the ending vertex of
iff the ending vertex of 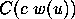 is the
vertex
is the
vertex 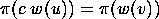 iff
iff
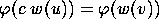 iff
iff
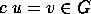 iff
iff

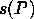 is the starting vertex of the path
is the starting vertex of the path 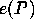 is the ending
vertex of it,
step (2.2.1) makes the path a loop,
this step may ``overfill'' the new (identified) vertex
because two or more edges of the same color may contain it,
this induces new identifications on the neighbors of the vertex
(to eliminate the extra edges),
this identifications must be propagated along the graph.
is the ending
vertex of it,
step (2.2.1) makes the path a loop,
this step may ``overfill'' the new (identified) vertex
because two or more edges of the same color may contain it,
this induces new identifications on the neighbors of the vertex
(to eliminate the extra edges),
this identifications must be propagated along the graph.
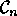 be the graph produced after
be the graph produced after 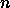 iterations before
entering the external loop (step (2)),
notice that in
iterations before
entering the external loop (step (2)),
notice that in 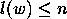 , where
, where 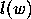 is the length of the word
is the length of the word 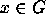 let
let 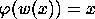 ,
then after at most
,
then after at most 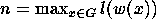 iterations the graph
iterations the graph 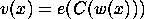 .
.
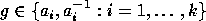 define
define 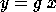 ,
we want to prove that after a finite number of iterations the vertices
,
we want to prove that after a finite number of iterations the vertices
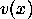 and
and 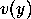 are joined by an edge of color
are joined by an edge of color 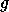 , we now that after
at most
, we now that after
at most 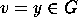 , but then there is a word
, but then there is a word 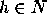 such that
such that
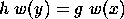 , but
, but
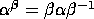 y
y
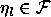 ,
but then after at most
,
but then after at most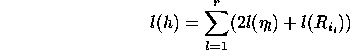
 after a finite number of
iterations (
after a finite number of
iterations (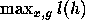 ) the graph
) the graph