Deva Van Der Werf
Bowdoin College, Brunswick, Maine
The Geometry Center, University of Minnesota
e-mail: dvanderw@polar.bowdoin.edu
August 1993
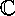 or to the Riemann sphere. Furthermore, it is this notion of angle that allows us to place a hyperbolic metric on the surfaces. Given a particular surface of genus
or to the Riemann sphere. Furthermore, it is this notion of angle that allows us to place a hyperbolic metric on the surfaces. Given a particular surface of genus 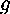 , we can study the finite-dimensional space of all conformally inequivalent Riemann surfaces (i.e. surfaces with different geometries), which is known as its Teichmüller space.
, we can study the finite-dimensional space of all conformally inequivalent Riemann surfaces (i.e. surfaces with different geometries), which is known as its Teichmüller space.
It was my intention to create a tool to move around in the Teichmüller space of a surface visually, i.e. to provide some sense of how a surface changes with different geometries upon it. The means I used to express the surfaces visually was a tiling of hyperbolic space; currently only the genus-2 case is available, and thus the tiling is by octagons. This project was suggested by David Ben-Zvi and Paul Burchard, both of whom have helped me greatly throughout the summer with the specifics of the project as well as general studies in the areas of complex analysis and hyperbolic geometry.