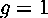 which does not necessitate hyperbolic geometry), while the C programs and the interface work only for the genus two case, at present.
which does not necessitate hyperbolic geometry), while the C programs and the interface work only for the genus two case, at present.
I developed Teichmüller Navigator as a NeXT application that would let a user ``navigate'' in the Teichmüller space of a two-holed torus. They would be doing this, if all went well, by being presented with a beginning tiling of a regular octagon. They could then click on any vertex they chose and drag it around. When this vertex had been moved into its new position and the mouse released the other vertices would be evolved into the nearest configuration that would produce a tileable polygon, yet still maintain the moved vertex in its new position.
The creation of this application involved four steps: writing the programs in Mathematica to evolve ``good'' polygons, transferring this into C, writing C code to create the tiles, and finally putting this all together with an interface. The Mathematica code is written to work for a surface of genus g (excluding the simple case of 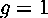 which does not necessitate hyperbolic geometry), while the C programs and the interface work only for the genus two case, at present.
which does not necessitate hyperbolic geometry), while the C programs and the interface work only for the genus two case, at present.
I began my attempt to find tileable polygons working in Mathematica because it was the only programming language I knew at the time, and I was already struggling to learn about hyperbolic geometry and Riemann surfaces. Once I had working (but very slow) programs in Mathematica , and was feeling more confident in the mathematics behind it, I began learning C and transferring the commands into it. The method used to evolve the code in both languages was essentially the same, although in Mathematica I was able to build off of the preexisting package ``Hyperbolic'' written by Oliver Goodman and Silvio Levy. Oliver Goodman also provided extensive guidance in both the use of the package, creating the methods to evolve the polygon, and my study of hyperbolic geometry in general.
As mentioned in the previous section, there are several conditions that must be true for a polygon to tile: the interior angles must sum 360 degrees (2 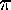 ), and identified sides must be of the same length. In order to evolve an initial ``bad'' polygon, I constructed an error function that evaluates these conditions. This error function returns the difference between the octagon's interior angles and 2
), and identified sides must be of the same length. In order to evolve an initial ``bad'' polygon, I constructed an error function that evaluates these conditions. This error function returns the difference between the octagon's interior angles and 2 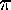 , and the differences between the lengths of the four pairs of identified sides. So moving within the sixteen-dimensional space of all octagons, we are actually trying to find the points that are zeros of this five-dimensional error function. To do this I used Newton's method (it was this portion of the code that took Mathematica so long to evaluate).
, and the differences between the lengths of the four pairs of identified sides. So moving within the sixteen-dimensional space of all octagons, we are actually trying to find the points that are zeros of this five-dimensional error function. To do this I used Newton's method (it was this portion of the code that took Mathematica so long to evaluate).
Having found a means to evolve a ``bad'' octagon into a ``good'' one, the next step was to tile hyperbolic space with that polygon. Tiles are created by transforming a given base polygon by various isometries. These are linear fractional transformations related to the side-pairings of the polygon. The standard polygon I began with included an arbitrarily chosen first point which determined the side-pairings of the various sides. Following the conventions of the Mathematica package ``Hyperbolic'' the sides were identified in groups of four (one to three, two to four, five to seven, six to eight) rather than in pairs of opposite sides, which would also have been a valid expression of the two-holed torus. If side one is paired with side three, then there is an isometry that takes side one to side three. This isometry will be representible by a three by three matrix, as it is the transformation matrix in the Minkowski model of hyperbolic space. A given point in the base polygon can be transformed by this matrix to its corresponding position in the tile that adjoins the base polygon along side three. Thus, the entire polygon can be transformed, to give the entire tile along side three. Another way of visualizing this is to imagine an axis of transformation: the arc through the midpoints of the two paired sides. Transforming the octagon is like shifting it along this axis, until side one is in the same position as side three of the base polygon.
For each of the pair of identified sides we can create an isometry and its inverse, which gives us a total of eight three-by-three matrices (call them 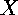 ,
, 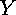 ,
, 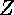 ,
, 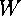 ,
, 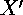 ,
, 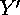 ,
, 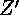 ,
, 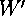 ). These isometries can be thought of as the generators of a group of isometries that tile the Poincaré disk. However, for the purposes of creating a ``Teichmüller Navigator'' we do not need an infinite tiling to the very boundary of the disk. This would be somewhat difficult to determine the isomtries for, and impossible to calculate and draw fast enough for an interactive-speed application. I chose to show only the first level of the tiling, i.e. the forty-eight tiles that touch the vertices of the initial octagon.
). These isometries can be thought of as the generators of a group of isometries that tile the Poincaré disk. However, for the purposes of creating a ``Teichmüller Navigator'' we do not need an infinite tiling to the very boundary of the disk. This would be somewhat difficult to determine the isomtries for, and impossible to calculate and draw fast enough for an interactive-speed application. I chose to show only the first level of the tiling, i.e. the forty-eight tiles that touch the vertices of the initial octagon.
These tilings are generated by the four side-pairing isometries. We can determine which combinations of them to take to get the first-level tiles for any octagon, then use these combinations plugging in side-pairing isometries calculated specifically for a particular evolved polygon. To determine which forty-eight combinations of these matrices are necessary for the first level tiling, I examined which transformations created the eight tiles around a given vertex. Consider a circular listing of the side-pairing isometries 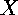 ,
, 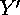 ,
, 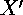 ,
, 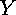 ,
, 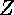 ,
, 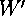 ,
, 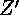 ,
, 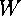 , the order in which we encounter them as we move counter-clockwise around the vertices starting at the first one. The combinations that will give the tiles about each vertex can be calculated by using a general rule, applied to each of the eight base isometries in turn. The procedure is to take the starting isometry, then the combination of it and the isometry previous in the list, then that combination of isometries and the second previous in the list, and finally those three and the fourth previous. This gives us the transformations for the four tiles we encounter moving counterclockwise around the vertex, away from the original octagon. The other three tiles around the vertex are found by taking the inverse of the next element in the list after of starting point, then the combination of that and the inverse of the next isometry after it, and lastly the combination of those two and the inverse of the third forward from the starting point. As an example of this, start with the isometry
, the order in which we encounter them as we move counter-clockwise around the vertices starting at the first one. The combinations that will give the tiles about each vertex can be calculated by using a general rule, applied to each of the eight base isometries in turn. The procedure is to take the starting isometry, then the combination of it and the isometry previous in the list, then that combination of isometries and the second previous in the list, and finally those three and the fourth previous. This gives us the transformations for the four tiles we encounter moving counterclockwise around the vertex, away from the original octagon. The other three tiles around the vertex are found by taking the inverse of the next element in the list after of starting point, then the combination of that and the inverse of the next isometry after it, and lastly the combination of those two and the inverse of the third forward from the starting point. As an example of this, start with the isometry 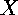 . Then we know that the other tiles around the same vertex as those will be
. Then we know that the other tiles around the same vertex as those will be 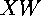 ,
, 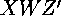 ,
, 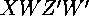 moving backward, and
moving backward, and 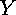 ,
, 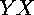 ,
, 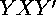 moving forward and taking inverses. We can apply this pattern starting at each of the eight isometries to compute forty-eight isometries of the base polygon that transform in to tile one level of the surrounding hyperbolic space (See Figure 2).
moving forward and taking inverses. We can apply this pattern starting at each of the eight isometries to compute forty-eight isometries of the base polygon that transform in to tile one level of the surrounding hyperbolic space (See Figure 2).
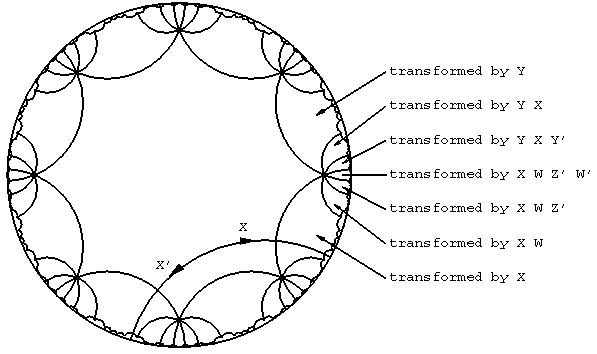
Figure 2: The eight isometries for a regular octgon, and and example of the combinations taken to tile around one vertex.
With code to both evolve octagons and tile the Poincaré disk, I was able to move on to constructing an actual interface, using NeXT Interface Builder and an immense amount of help from Paul Burchard. This interface, ``Teichmüller Navigator'', allows the user to view an initial tiling with regular octagons, which they may then tweak and pull into different configurations. As I stated above, these ``different'' tilings will not necessarily be different Riemann surfaces- their may be different tilings representing the same point in the Teichmüller space of a surface (though each point of the Teichmüller space is represented in the space of all tilings). In fact, it is even possible to manipulate the initial octagon so that it appears to have been transformed by one of the eight base isometries. We can get a wide variety of tilings with the program (See Figure 3).
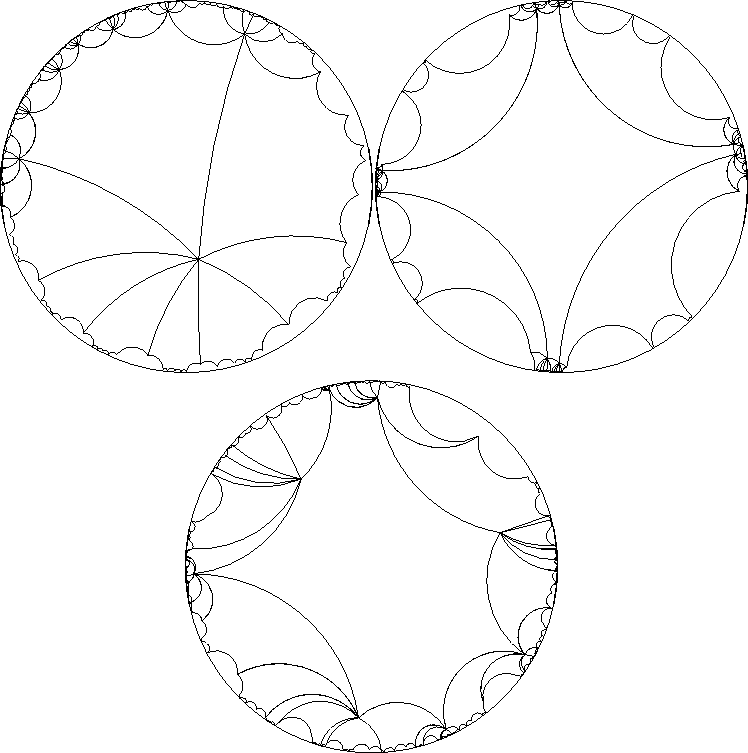
Figure 3: Some sample tilings.
It is interesting to note that some of the octagons verge on degenerate tilings. When one vertex is pulled open so that it is nearly a straight line, it has almost reached the point where the evolution may snap it concave (See Figure 4).
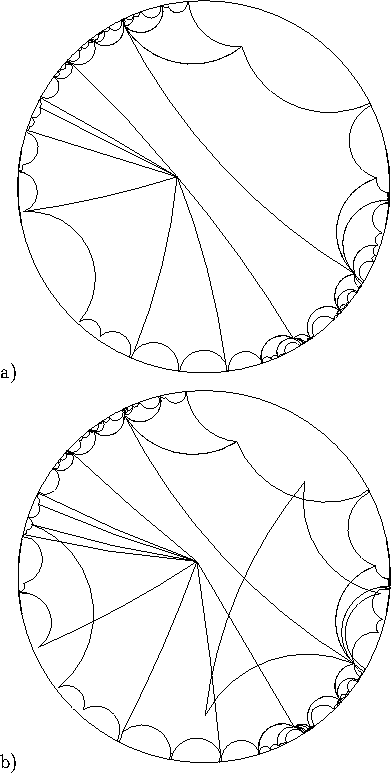
Figure: Pushing the boundaries of Teichmüller space. a) a nearly degenerate octagon, and b) a ``bad'' convex octagon that does not tile.
We can imagine that this corresponds to some Riemann surface (some point in Teichmüller space) that is almost at the point that there will no longer be a conformal map from it to  . Perhaps one of the handles has been narrowed and stretched so that it has almost been pulled apart. Hopefully, in the future we can integrate some means to see the Riemann surfaces given by the tilings as the surfaces embedded in three space, i.e. as ``doughnuts''. This would allow us to get a better idea of what was actually happening to the surface at these interesting points in its Teichmüller space.
. Perhaps one of the handles has been narrowed and stretched so that it has almost been pulled apart. Hopefully, in the future we can integrate some means to see the Riemann surfaces given by the tilings as the surfaces embedded in three space, i.e. as ``doughnuts''. This would allow us to get a better idea of what was actually happening to the surface at these interesting points in its Teichmüller space.