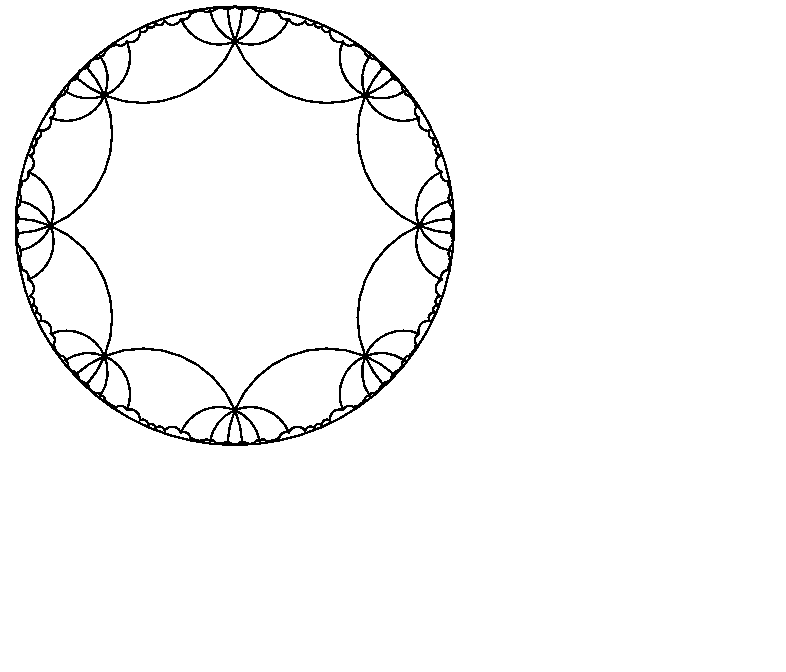
Figure: A tiling of the Poincaré disk by regular octagons.
One way of examining topological surfaces is by ``cutting them up'' and flattening them out on a plane. The easily-visualized example of this is the genus 1 case, the one-holed torus. Making one straight cut produces a cylinder, which can be cut open yet again to produce a rectangle with opposite sides identified. This is a common depiction of the torus, in which movement on the surface is simulated by a line off one side being wrapped around and coming back in on the opposite. To get an even better picture of the torus we can tile the plane with the rectangle, so that we do not have to wrap our movements around, but rather can move anywhere in the plane and still be on a copy of the original tile, i.e. on the surface. We can even change the angles of the recangle to make it a parallelogram, and still tile with it nicely.
When we move up one genus to the two-holed torus, however, cutting the surface open creates an octagon. To see that this is indeed the case imagine beginning with an octagon and gluing together the first and third, second and fourth, fifth and seventh, and the sixth and eighth sides. We see that the octagon is a more interesting case when we begin trying to tile the plane. The sum of the interior angles of an octagon in the Euclidean plane is 1080 degrees. So in the regular case, each angle will be 135 degrees. But we cannot fit an integer number of such octagons around a vertex! If we take two copies of the octagon and join them along one edge we will already have 270 degrees around a vertex, so we cannot fit even one more copy into the remaining 90 degrees. And to achieve a tiling that will simulate the genus-two surface we would like to fit eight tiles around each vertex! The solution to this problem is that we must attempt our tiling in a space that allows octagons to have interior angle sums of 360 degrees; in the regular case, we need an octagon with eight equal sides and eight angles of 45 degrees each.
The answer to our problems is hyperbolic geometry. Hyperbolic geometry arose from the idea that perhaps a valid system of theorems and manipulations could be based on a variation of the standard postulates of Euclid. The only difference between the two base sets of assumptions is in the parallel axiom. Euclid's original postulate proposed that for a line and a point not on the line, there is only one line through that point that is parallel to the original. Alternatively, in hyperbolic geometry there are many lines through a point that do not intersect a line not containing that point.
To visualize the hyperbolic plane we will use what is known as the Poincaré disk model. This is constructed on the unit disk, with straight lines given as arcs of circles orthogonal to the boundary of the disk, or in some cases as diameters. In this model, it is not intuitively obvious what the distance is between any two points, because there is a hyperbolic metric on the disk. An arc (line) segment that is close to the boundary appears shorter than one oif the same length near to the center of the disk. Furthermore, if we are considering the intersection of two arcs (lines) we see that by pulling the point at which they intersect toward the boundary, we can make the angle arbitrarily smaller. Thus we can see that if we take a regular polygon, with all sides of equal length, and we pull the vertices toward the boundary of the disk, we can decrease the angle at each to 45 degrees. Though we will have lengthened the sides, they will still be equal to one another. Using polygons in such a space, we can examine how to depict different Riemann surfaces visually as tilings.

Figure: A tiling of the Poincaré disk by regular octagons.
In addition to the Poincaré disk model of hyperbolic space, we will also be using the Minkowski or hyperboloid model to do a number of calculations within. In this model, each point on the Poincaré disk is expressed by three coordinates, and can be thought of as sitting somewhere on the upper sheet of the hyperboloid 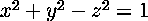 . There is a simple conversion that will take a point in the Poincaré disk model to the Minkowski, and vice versa. The advantage to working within this model of hyperbolic space is that the Minkowski metric is much simpler than that of the Poincaré disk, and thus many of the calculations become simpler in it.
. There is a simple conversion that will take a point in the Poincaré disk model to the Minkowski, and vice versa. The advantage to working within this model of hyperbolic space is that the Minkowski metric is much simpler than that of the Poincaré disk, and thus many of the calculations become simpler in it.
Once we have hyperbolic space to work within, our question is which polygons are actually tileable. Take the case of the octagon (two-holed torus). Each octagon can be expressed by sixteen values, two coordinates for each vertex. So the space of all possible octagons is sixteen-dimensional. But we must place certain restrictions on exactly how the sixteen values are chosen to define the octagon so that it will tile.
If we imagine gluing up our polygon into a surface embedded in three space, we can see what some of these conditions will be. When the octagon is glued together the vertices will all become one point on the surface. We know that there must be 360 degrees around a vertex. Thus, the interior angles of the octagon must sum 360 degrees so that when it is glued up this will be true. In gluing up the octagon we also see that the sides that are glued together (identified with each other) must be of equal length. This gives us one angle condition and four side-pairing conditions, which restricts the sixteen-dimensional space of all octagons to an eleven-dimensional space of octagons that will work in tiling the Poincaré disk.
How does this space relate to the Teichmüller space of the two-holed torus? We will see that it actually projects onto the Teichmüller space. This is implied by the Uniformization Theorem, which states that the universal cover of any Riemann surface of genus 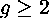 is conformally the unit disk. From this we know that each Riemann surface (each point in the Teichmüller space) is given by at least one tiling in hyperbolic space. Thus there is a tiling that corresponds to every conformal structure on a surface- in fact, there are many. Three of these extra dimensions of tilings beyond those that represent the Teichmüller space of the surface are given by the Möbius transformations that allow rotations and translations of the polygon. Moving within the space of all octagons that tile, we will find some tileable polygon that may actually represent the same Riemann surface as another valid tiling, yet be rotated by some amount, or translated in some direction so that they appear to be different. So with these three translations/rotations, and our previous five conditions of angle sum and side-pairings, we have accounted for eight of the sixteen dimensions in the space of all octagons.
is conformally the unit disk. From this we know that each Riemann surface (each point in the Teichmüller space) is given by at least one tiling in hyperbolic space. Thus there is a tiling that corresponds to every conformal structure on a surface- in fact, there are many. Three of these extra dimensions of tilings beyond those that represent the Teichmüller space of the surface are given by the Möbius transformations that allow rotations and translations of the polygon. Moving within the space of all octagons that tile, we will find some tileable polygon that may actually represent the same Riemann surface as another valid tiling, yet be rotated by some amount, or translated in some direction so that they appear to be different. So with these three translations/rotations, and our previous five conditions of angle sum and side-pairings, we have accounted for eight of the sixteen dimensions in the space of all octagons.
For two last degrees of freedom, consider the ``glued-together'' version of our example- the octagon. Remember that the vertices will all end up being identified to the same point on the surface; this is the point at which we begin cutting up the surface to create the polygon. We are free to move this initial cutting point around on the surface, which is two-dimensional. This means that in looking at various tilings we may find two different octagons that both represent the same Riemann surface, i.e. the same point in the Teichmüller space, simply produced by different initial cutting locations.
When considering the higher genus cases, these basic concepts will still hold true. For a genus-g surface, the space of all tiling 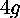 -gons will be
-gons will be 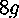 . There will still be five extra dimensions due to the three Möbius transformations and the movement of the point at which we begin cutting. But there will be the same angle condition, and in addition there will be
. There will still be five extra dimensions due to the three Möbius transformations and the movement of the point at which we begin cutting. But there will be the same angle condition, and in addition there will be 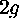 side-pairing conditions. If these additional conditions and degrees of freedom are taken into account, we see that:
side-pairing conditions. If these additional conditions and degrees of freedom are taken into account, we see that:

If we take into account that we will be seeing some tilings that are actually just rotations, translations, and different base cutting points of the same Riemann surface. So the space that we are actually moving around in is 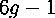 dimensional, but the space of tilings that actually represent different Riemann surfaces (points in Teichmüller space) is of dimension
dimensional, but the space of tilings that actually represent different Riemann surfaces (points in Teichmüller space) is of dimension 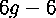 . It is actually known that the Teichmüller space of genus-g surfaces is a
. It is actually known that the Teichmüller space of genus-g surfaces is a 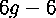 dimensioned ball, so it seems that our analysis is sensible.
dimensioned ball, so it seems that our analysis is sensible.