 (1M mpeg)
(1M mpeg)
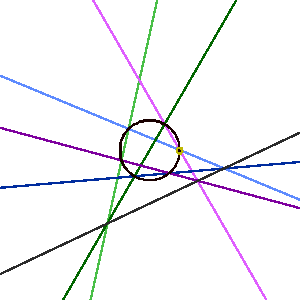
Consider the following diagram of Pascal's theorem. The order of the edges is green, blue, purple, green, blue, purple: first the light version of each color, then the dark. The Pascal line is in gray. Now click on the picture and see how it changes.
In the movie we pulled the pink (light purple) line out to infinity and brought it back. Now let's take another diagram of Pascal's theorem, this one with a tangent line. Click on this diagram to see what happens when we move the (dark) purple line out to infinity:
But what does it mean to pull a line out to infinity? Remember that we can represent points and lines in the projective plane by points and great circles on the unit sphere. This corresponds to the more usual representation of the projective plane when we project the sphere onto one of its tangent planes.
We begin with the unit sphere x^2+y^2+z^2=1. We use the center of the sphere to project it onto the plane tangent to the sphere at the north pole. This plane is the plane z=1; every point on the upper hemisphere goes to a point on this plane in the obvious way. The point on the equator of this sphere (those points for which z=0) become the points of infinity in the plane z=1; they project onto points infinitely far away from the z-axis.
So now we imagine our diagram of Pascal's theorem represented on the unit sphere. We start with a conic, which is a small circle on the unit sphere. Lines going through the conic are great circles passing through the small circle; our Pascal line is another great circle. Then we rotate this sphere about the origin, leaving the tangent plane z=1 in place. Different great circles on the sphere pass through the xy-plane, and as they do so they go out to infinity in the tangent plane.
These are just some of the many possible affine interpretations of Pascal's Theorem. The conic could be an ellipse, parabola, or hyperbola; the inscribed hexagon could be convex or non-convex. One or more of the vertices of the hexagon could be repeated, giving rise to tangent lines.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: Nov 30 1995 ---
Last modified: Thu Nov 30 15:37:14 1995