Next: Some Stronger Theorems
Prev: Pascal's Theorem
Up: Projective Conics
Brianchon's Theorem
Another way of stating Pascal's theorem is: If points ABCDEF
lie on a conic, then points AB.DE, BC.EF, and
CD.FA lie on one line. This shows the way to a dual theorem,
known as Brianchon's theorem: if lines abcdef lie on a conic,
then lines (a.b)(d.e), (b.c)(e.f), (c.d)(f.a) lie
on one point. If six lines lie on a conic, then the hexagon which
they form circumscribes the conic. So the more traditional form of
Brianchon's theorem is:
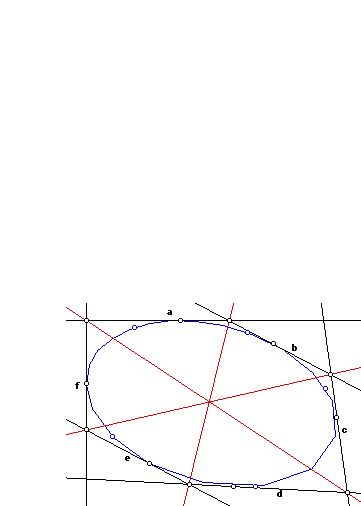
If a hexagon is circumscribed about a conic, its diagonals
are concurrent.
Brianchon's theorem has a converse, too:
If the diagonals of a hexagon are concurrent, then the
hexagon may be circumscribed about a conic.
The proofs for these are exactly the duals of the proofs
for Pascal's theorem and its converse.
Next: Some Stronger Theorems
Prev: Pascal's Theorem
Up: Projective Conics
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: Nov 30 1995 ---
Last modified: Thu Nov 30 15:30:47 1995


![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page