Surfaces in Cylindrical Coordinates

In the following, you may want to use Maple to plot some surfaces in polar coordinates. The command plot3d with the option coords=cylindrical will be useful for plotting functions of the form r=f(theta,z).

Let C(r,theta,z)= [ r cos(theta), r sin(theta), z ] be the mapping into cylindrical coordinates.

Recall that if a surface is parametrized by S(s,t)=[ r(s,t), theta(s,t), z(s,t) ] then the tangent plane (if it exists) to the image of S is spanned by the two vectors u=dS/ds and v=dS/dt. The image of the surface in cylindrical coordinates therefore has tangent vectors given by DC u and DC v.

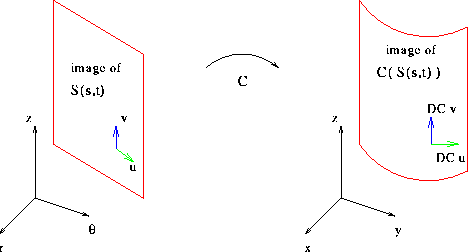
Figure 1. Geometry of Cylindrical coordinates.

Question #1

• A cylinder
• A vase (Hint: Try a cubic function of z. You do not need to worry about the bottom of the vase, ie, the vase doesn't need to hold water. We've provided an additional hint if you need it.)

• Parametrize a tangent plane to the surface at theta=Pi and z=0.
• Sketch the tangent plane on the surface.