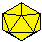


 12
12 

 12
12 

 12
12 


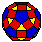
 12
12  30
30 
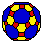
 12
12  30
30 
| F = # of faces E = # of edges V = # of vertices |
| Model | F | E | V | Shapes |
| Icosahedron | ||||

| 20 | 30 | 12 | 20  |
| Truncated Icosahedron | ||||

| 32 | 90 | 60 | 20  12 12  |
| Icosadodecahedron | ||||

| 32 | 60 | 30 | 20  12 12  |
| Truncated Dodecahedron | ||||

| 32 | 90 | 60 | 20  12 12  |
| Dodecahedron | ||||

| 12 | 30 | 20 | 12  |
| Rhombicosadodecahedron | ||||

| 62 | 120 | 60 | 20  12 12  30 30  |
| Rhombitruncated Icosadodechedron | ||||

| 62 | 180 | 120 | 20  12 12  30 30  |
 = blue regular decagon (10-sides)
= blue regular decagon (10-sides)
We have picked icosahedron and rhombicosadodecahedron to show the 2-, 3-, and 5- fold symmetries in this group. In each of the polyhedra below, we have highlighted some planes of reflection symmetry to show the folds of symmet$
| 2-fold | 3-fold | 5-fold |
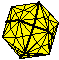
| 
|  |

| 
|  |