The Conic as a Locus of Lines
We defined a conic as the set of points of intersection of
corresponding lines in two projective pencils. This prompts an
inquiry into the dual figure: the set of lines joining
corresponding points on two projective point ranges. Before
we can do this, we need to define some terms. A line is
tangent to a curve (set of points) if exactly one point
lies on both the line and the curve. A set of points, or curve,
is the envelope of a set of lines if each point lies on
exactly one line and each line lies on exactly one point. Then
each line in the set will be tangent to the curve.
The envelopes that we will want to study have a familiar
interpretation in string art. We set up hooks on two straight
objects, and place strings between corresponding hooks, noting
the curve that the strings trace out. Durer gave the following
diagram:
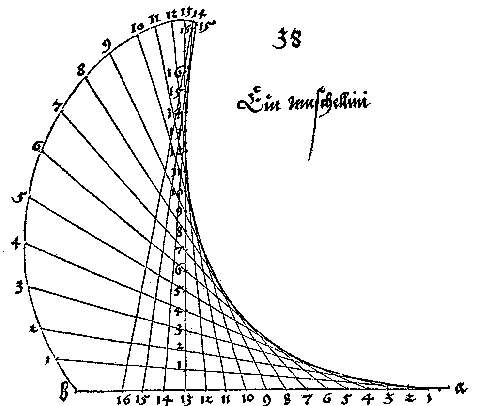
The curve on the right, traced out by lines connecting
corresponding points on the horizontal and vertical lines, is
a parabola. (For more on Durer,
click here.) We can describe it easily using coordinates;
it is the locus of lines connecting points (-a,0) to (-13,a).
Connecting points (a,0) to (0,1/a) in a similar way gives a
hyperbola:

Connecting points (a,0) to (1/a,1) gives an ellipse:
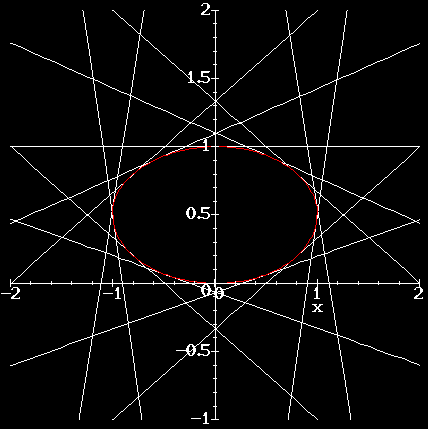
So now it seems that the envelope of the lines connecting
corresponding points on two projective point ranges is a
conic. Now we define such an envelope as a line
conic, and need to prove that any line conic is a point
conic and vice versa. We can
prove this now using coordinates and calculus; we will
present synthetic proofs in following sections.