Peaucellier's Linkage

Part 3. Another look at the Linkage

A. The linkage and inversion

1. Compare the chart you made in the section on inversion to the shapes traced out by P and Q. Is it possible that P and Q are related by inversion? If so, what can you say about the relationship of the center of the circle of inversion to the shapes traced by P and Q?

2. Recall the definition of inversion through a circle of radius r centered at A. The inverse F' of a point F is such that:

   A, F, and F' are collinear, and (AF)(AF') = r^2.

   Find the center of the circle of inversion and verify that Q is related to P by inversion. (Hint: You may want to use the Calculator on the Measure menu to measure a product. What has to be true of this constant as P moves?)

The above investigations helped you to find the center of the circle of inversion through which P and Q are related. In the following we will see how to find the radius of this circle.

B. Constructing the circle of inversion

Using the definition of inversion and Sketchpad's Calculate option, you can compute the radius of the center of inversion. What is it?

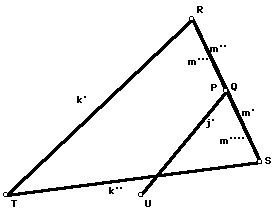
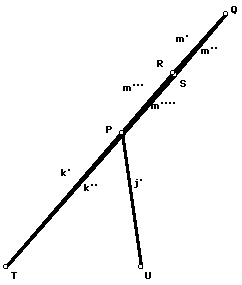
Since the radius is a constant independent of the position of the linkage, it depends only on the three fixed length segments you made off to the side. What is the relationship? This is a pen and paper exercise using the Pythagorean theorem. Below are some pictures of specific cases to help you form a conjecture for a general equation for the radius of the circle of inversion. In the first picture, P and Q lie on top of each other. In the second, R and S lie on top of each other. In each case, state how the radius of the circle of inversion is related to the segments j, k, and m.

You should now have discovered a relationship between the radius of the circle of inversion and the lengths of j, k, and m. You can prove that that relationship holds in the two special cases shown above; how would you prove that it holds for any configuration of the linkage?

You might now use Sketchpad's Translate by Marked Distance option to construct the circle of inversion. However, that would be a ruler and compass construction; geometry purists prefer to construct things using only a straightedge and compass. (If we know we can construct something using a straightedge and compass, we know something more about its coordinates than if we used a ruler. Also, the more we know about the construction of an object the more easily we can prove it has the properties we desire.)

Use what you have learned to construct a segment whose length is the same as the radius of the circle of inversion. Try to use only straightedge and compass (Suggestion: sketch the object you wish to construct on paper and plan your construction before using the computer.) Construct the circle of inversion and use your method for constructing the inverse of a circle to construct the shape you expect Q to be constrained to. Check that Q does stay on this shape as you move P.

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@geom.umn.edu
Created: Jun 09 1996 --- Last modified: Tue Apr 15 16:09:33 1997