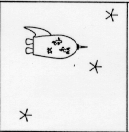
Remember the fly on the brick wall from the last lab? It got ambitious and tried to land on my bagel. I swatted it off, and it landed on the wall. It's still a bit disoriented and can't move around very well. All it can see is one piece of the wallpaper pattern. Here's what it sees:

What might the wallpaper pattern look like, if this were a motif for it?
There's no way to tell for sure. We saw two examples of possible patterns on a page of last week's lab. The orbifold could be this pattern with both of its sides glued together (a torus) or one pair of sides could be glued with a twist to form a klein bottle.
What happens if some of the sides of the square are mirror boundaries on the orbifold of the wallpaper pattern? What orbifold do you get by glueing a pair of adjacent sides together? What if both pairs of opposite sides are joined with a twist? ... How may ways can you think of to make an orbifold out of this motif?
Shown below are several different squares with directions for constructing orbifolds. When the instructions say "with a twist", the construction of the orbifold involves a Moebius strip.
If you had several copies of this motif, you could patch them together according to the directions to get a plane pattern. For example, when the instructions say to connect the top of the square to its bottom, you can join two separate squares top to bottom to start your plane pattern. Notice that for some of the patterns you will need mirror image motifs as well.
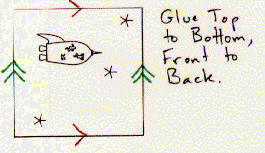
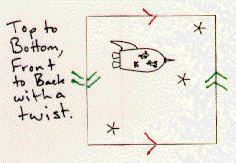
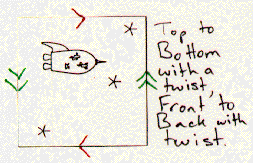
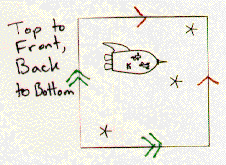
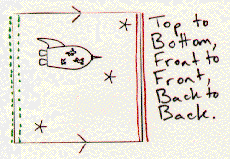
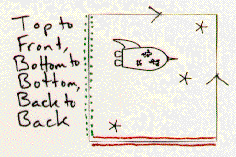
Exercise: Copy the motifs onto transparencies. Have each person in your group construct a different pattern -- you will find some (but not all) of the possible patterns for the bug's wallpaper. This information will be very useful to the poor fellow as he makes his way home!
Exercise: What orbifold does each of the motifs above represent? What plane pattern corresponds to that orbifold? Does this agree with your results from the previous exercise? How many of the orbifolds of the seventeen wallpaper patterns that you discovered in your homework can be constructed by identifying sides of a square motif?
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Heidi Burgiel
Comments to:
webmaster@geom.umn.edu
Created: Dec 7 1995 ---
Last modified: Wed May 28 11:34:48 1997
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.