
Question: Suppose a two copies of a figure are slapped down in the plane. Specify a way to find a reflection, a rotation, and a translation whose product takes one copy of the figure to the other. Here are two examples to work on with pencil and paper. Remember--- you might not need all three operations!

Some of the theorems on this page are left to you to complete. You can discover the missing pieces of each of them using the Geometer's Sketchpad. Even if you can determine the theorem statements without the software, think about how you would demonstrate them using Sketchpad. In particular, what elements of the sketch should be arbitrarily placed and what elements need to depend on other elements? How would you design your sketches to most effectively teach these concepts to your students?
Theorem 1 The product of any two reflections in the plane is a translation or rotation. In particular, if the mirror lines ............ their product is a translation by a vector ......................................................................; if the mirror lines ........., their product is a rotation through an angle ............................... with the center of rotation at .................................
Your Sketchpad sketch would begin with something like the following:
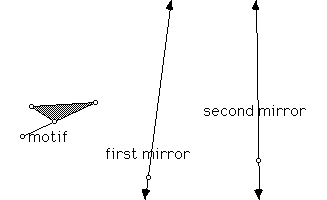
Theorem 2: Any translation is the product of two carefully chosen reflections.
To illustrate this, begin with a motif and some line segment representing the translation. Construct a pair of reflections whose product is the translation.
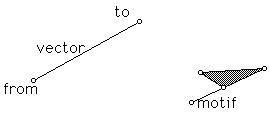
Theorem 3: Any rotation in the plane is the product of two reflections.
To illustrate this, start with a motif and something representing an angle and center of rotation. Construct a pair of reflections whose product is the rotation.
Theorem 4: Any transformation is the product of just three reflections!
This says that Theorem 0 could be restated: any product of a reflection, a rotation and a translation is equivalent to the product of three carefully chosen reflections. You'll be asked to find such a product of reflections in your homework. The next problem also appears on the homework.
Theorem 5: Given a pair of isometries A and B, the product AB is not necessarily the same as the product BA.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Chaim Goodman-Strauss, revised and edited by Heidi Burgiel
Comments to:
webmaster@geom.umn.edu
Created: Dec 7 1995 ---
Last modified: Jun 11 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.