
We have not yet discussed handles (denoted by an "o" in the notation) and cross caps (denoted "x"). The next two examples should help explain what characteristics of a pattern might cause these to appear in the orbifold notation for that pattern.
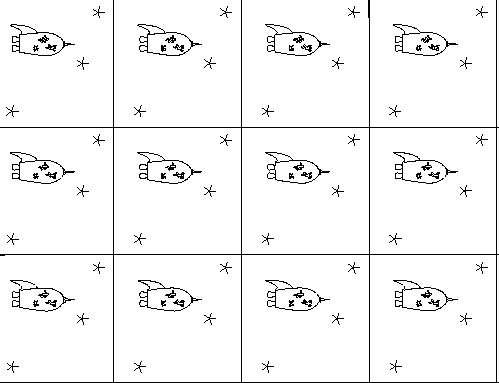
Exercise: Copy the picture shown above onto a transparency. What do you need to do to make two identical images lie on top of each other? Is there more than one way that you can do this?
Because you are limited by the material of the transparency, it is difficult to determine what the orbifold of this pattern would be. However, you should have noticed that rolling the pattern up into a tube either vertically or horizontally brings identical points together. Is there a way we can roll the sheet up both vertically and horizontally?
In theory, there is. First imagine rolling the pattern up into a horizontal tube whose circumference is exactly the size of one motif (try it!). All the vertically translated copies of the motif have now been identified -- we only have to superimpose all the horizontally translated copies of the motif to complete our orbifold.
To accomplish this, imagine stretching and bending your tube into a donut, whose inner and outer circumferences are exactly the width of one motif. This is impossible to do without ripping a paper pattern, but an ideal mathematical surface could do this. This donut or "torus" is our orbifold. See the Geometry Center's Topological Zoo for a detailed description of a torus

The picture above (from The Shape of Space video) depicts the orbifold of the first spaceship pattern. This orbifold is reminiscent of a handle or ring. In fact, if you put a handle on a sphere you would get a surface that's "topologically equivalent" to our donut. When a topologist wishes to describe a surface, she or he will often do it by describing the surface as a sphere with several added features. The orbifold notation uses this convention to describe the surfaces that are orbifolds -- this torus and the corresponding symmetry group is denoted by a "o" in the orbifold notation.
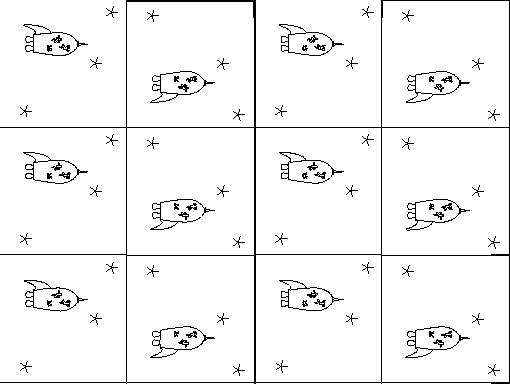
Exercise: Copy the picture shown above onto an overhead transparency. What do you have to do to identify an image of the spaceship motif with the image directly above it?
Exercise: Cut a horizontal strip of images out of your picture. Can you connect the ends of the strip so that when proceeding along the strip and accross the splice you encounter a seemingly infinite sequence of space ships, alternating right side up then upside down? What shape does the strip make?
In one direction, this pattern has translational symmetry. In the other, it has glide reflective symmetry. We can identify the images above and below each image with that same image by rolling the pattern into a tube as we did in the previous section. How do we identify horizontal images?
Study a motif and the image to its right. The "back end" of the image is glued to the "front end" of the motif, but upside down. When we rolled the pattern into a tube, the top of a motif was identified with the bottom of that same motif. Can we somehow identify the front with the back in the same way?
By putting a twist in before we make the identification, we can. If we stretch and twist our motif into a Moebius strip (remember, we're working with an ideal surface, and not a real piece of paper) we can glue its front to its back, upside down.
To visualize the entire orbifold, imagine taking the tube obtained by identifying the top and bottom of the motif and pushing one end through into the interior of the tube. If you then glue the two ends of the tube together, you get a Klein bottle.
If we wish to describe the Klein bottle in terms of modifying the sphere, what we have to do is add two cross caps to the sphere. A cross cap is formed by glueing an (ideal) round patch to the boundary of the Moebius strip. You can get a feel for what happens when you attempt this by crocheting along the boundary of a Moebius strip then decreasing. (Crocheted Moebius strips make unique gifts at baby showers!)
You may recall that the symbol for a cross cap in the orbifold notation is an "x". The symbol for the orbifold of the Klein bottle and for the symmetry of the corresponding pattern is "xx". These cross caps may seem mysterious, but they are very useful in identifying symmetry groups!
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Heidi Burgiel
Comments to:
webmaster@geom.umn.edu
Created: Dec 7 1995 ---
Last modified: Jun 11 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.