Lab #11
This worksheet does not need to be handed in, but you are responsible
for the material.
The purpose of the lab is to understand how a change of coordinates
transforms points, curves, tangent vectors, and area.
Recall that the polar transformation,
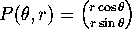 takes a point in the
takes a point in the
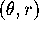 -plane and sends it to a point in the
-plane and sends it to a point in the 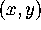 -plane. It
follows that P takes a parametric curve
-plane. It
follows that P takes a parametric curve 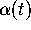 in the
in the
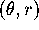 -plane and maps it to a curve,
-plane and maps it to a curve, 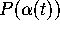 , in the
, in the
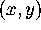 -plane. Similarly, the Jacobian of the transformation, DP,
takes a velocity vector to the parametric curve, call it
-plane. Similarly, the Jacobian of the transformation, DP,
takes a velocity vector to the parametric curve, call it 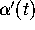 ,
and sends it to a velocity vector,
,
and sends it to a velocity vector, 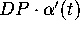 , of the image
curve
, of the image
curve 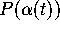 .
.
ACTIVITY 1: Inventing a Polar Curve
Think of any continuous function on the interval 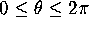 .
(For example, you might choose
.
(For example, you might choose 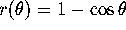 .)
For later reference, be sure to write down the function that you used!
Before coming to class,
each student should carefully sketch the image under P of the graph of
the chosen function on a clean sheet of paper (or, better yet, get a
computer printout). This curve will be in the
.)
For later reference, be sure to write down the function that you used!
Before coming to class,
each student should carefully sketch the image under P of the graph of
the chosen function on a clean sheet of paper (or, better yet, get a
computer printout). This curve will be in the 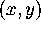 -plane; we
will use this curve in a later activity.
-plane; we
will use this curve in a later activity.
ACTIVITY 2: Sketching Preimages of Curves
For each of the two curves in Figure  ,
sketch a curve in the
,
sketch a curve in the 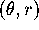 -plane that is mapped to a
corresponding curve in Figure
-plane that is mapped to a
corresponding curve in Figure  . The curve in the
. The curve in the
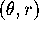 -plane is called the preimage.
Check your guesses with a
graphing calculator or with maple (see ?plot,polar).
(Hint: The first
curve in Figure
-plane is called the preimage.
Check your guesses with a
graphing calculator or with maple (see ?plot,polar).
(Hint: The first
curve in Figure  is the image of a graph, the second curve is
the image of a parametric curve.)
is the image of a graph, the second curve is
the image of a parametric curve.)
ACTIVITY 3: Another Preimage of a Curve
By this point, your instructor will have collected your
curve from the first activity. When you get to this activity, your
instructor will give you
a curve that someone else in the
class sketched.
Can you figure out an approximate preimage of this curve?
ACTIVITY 4: Images of Horizontal and Vertical Tangent Vectors
Suppose that a parametric curve in the 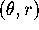 -plane has a horizontal
tangent vector,
-plane has a horizontal
tangent vector, 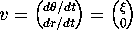 . Then
the image of this vector under
DP is a vector of the form
. Then
the image of this vector under
DP is a vector of the form 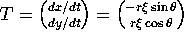 . Notice that T is a
linear multiple of the vector
. Notice that T is a
linear multiple of the vector 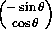 which is the direction of increasing
which is the direction of increasing 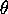 .
.
- For the curve in Figure
 .A, mark the locations on the
curve that are the images of the
.A, mark the locations on the
curve that are the images of the
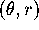 values at which
values at which 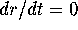 . Use your result from
Activity 2 to explicitly compute the vectors T at those points.
. Use your result from
Activity 2 to explicitly compute the vectors T at those points.
- If a parametric curve in the
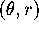 -plane has a vertical
tangent vector v, write down the direction of
-plane has a vertical
tangent vector v, write down the direction of
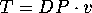 . Mark locations on Figure
. Mark locations on Figure  .B for which the
preimage of T is vertical.
.B for which the
preimage of T is vertical.
ACTIVITY 5: Preimages of Horizontal and Vertical Tangent Vectors
- What equation must a tangent vector at
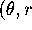 ) satisfy if it is
mapped by DP to a horizontal vector? Verify your conjecture for
Figure
) satisfy if it is
mapped by DP to a horizontal vector? Verify your conjecture for
Figure  .A, using the fact that the curve through
.A, using the fact that the curve through 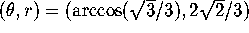 has the tangent vector
has the tangent vector 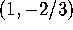 . (Why this point and vector?)
. (Why this point and vector?)
- What equation must a tangent vector at
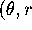 ) satisfy if it is
mapped by DP to a vertical vector?
Verify your conjecture for Figure
) satisfy if it is
mapped by DP to a vertical vector?
Verify your conjecture for Figure  .A, using
the fact that the curve through
.A, using
the fact that the curve through
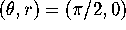 has the tangent vector
has the tangent vector
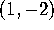 .
.
ACTIVITY 6: Transforming Area
What is the approximate area of a small square of side length s
based at the point 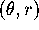 ? Test your conjecture by applying the
matrix
? Test your conjecture by applying the
matrix 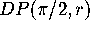 to the vectors
to the vectors 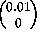 and
and 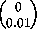 for
for 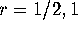 , and 2.
, and 2.
ACTIVITY 7: Bonus Activity
Prior to February 14th (Valentine's Day), figure out the parametrization
of a curve in the  -plane whose image under P is a
heart-shaped curve (with two cusp points).
-plane whose image under P is a
heart-shaped curve (with two cusp points).
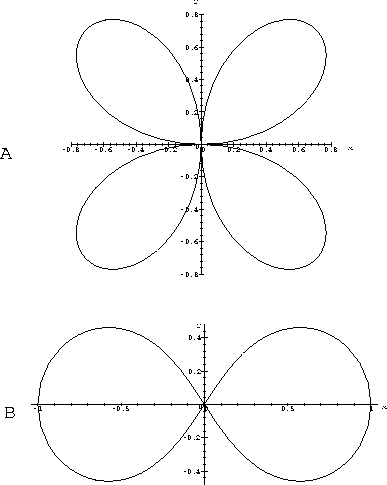
Figure: Two curves that are images under P of curves
in the 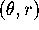 -plane.
-plane.
About this document ...
Return to Labs Homepage
Return to Calculus 3353/3354 Homepage
URL: http://www.geom.umn.edu/~math335x/Labs/Lab10/Lab10.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to:
hesse@math.umn.edu
Last modified: Feb 20, 1997
The University of Minnesota is an equal opportunity educator and employer.
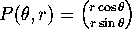 takes a point in the
takes a point in the
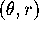 -plane and sends it to a point in the
-plane and sends it to a point in the 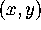 -plane. It
follows that P takes a parametric curve
-plane. It
follows that P takes a parametric curve 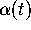 in the
in the
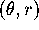 -plane and maps it to a curve,
-plane and maps it to a curve, 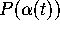 , in the
, in the
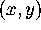 -plane. Similarly, the Jacobian of the transformation, DP,
takes a velocity vector to the parametric curve, call it
-plane. Similarly, the Jacobian of the transformation, DP,
takes a velocity vector to the parametric curve, call it 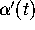 ,
and sends it to a velocity vector,
,
and sends it to a velocity vector, 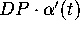 , of the image
curve
, of the image
curve 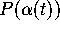 .
.
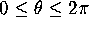 .
(For example, you might choose
.
(For example, you might choose 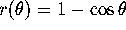 .)
For later reference, be sure to write down the function that you used!
Before coming to class,
each student should carefully sketch the image under P of the graph of
the chosen function on a clean sheet of paper (or, better yet, get a
computer printout). This curve will be in the
.)
For later reference, be sure to write down the function that you used!
Before coming to class,
each student should carefully sketch the image under P of the graph of
the chosen function on a clean sheet of paper (or, better yet, get a
computer printout). This curve will be in the  -plane; we
will use this curve in a later activity.
-plane; we
will use this curve in a later activity.
 -plane that is mapped to a
corresponding curve in Figure
-plane that is mapped to a
corresponding curve in Figure 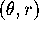 -plane is called the preimage.
Check your guesses with a
graphing calculator or with maple (see ?plot,polar).
(Hint: The first
curve in Figure
-plane is called the preimage.
Check your guesses with a
graphing calculator or with maple (see ?plot,polar).
(Hint: The first
curve in Figure 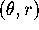 -plane has a horizontal
tangent vector,
-plane has a horizontal
tangent vector, 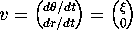 . Then
the image of this vector under
DP is a vector of the form
. Then
the image of this vector under
DP is a vector of the form 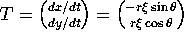 . Notice that T is a
linear multiple of the vector
. Notice that T is a
linear multiple of the vector 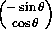 which is the direction of increasing
which is the direction of increasing 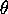 .
.
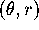 values at which
values at which 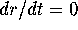 . Use your result from
Activity 2 to explicitly compute the vectors T at those points.
. Use your result from
Activity 2 to explicitly compute the vectors T at those points.
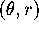 -plane has a vertical
tangent vector v, write down the direction of
-plane has a vertical
tangent vector v, write down the direction of
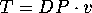 . Mark locations on Figure
. Mark locations on Figure 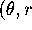 ) satisfy if it is
mapped by DP to a horizontal vector? Verify your conjecture for
Figure
) satisfy if it is
mapped by DP to a horizontal vector? Verify your conjecture for
Figure 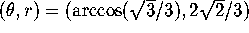 has the tangent vector
has the tangent vector 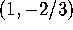 . (Why this point and vector?)
. (Why this point and vector?)
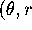 ) satisfy if it is
mapped by DP to a vertical vector?
Verify your conjecture for Figure
) satisfy if it is
mapped by DP to a vertical vector?
Verify your conjecture for Figure 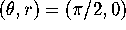 has the tangent vector
has the tangent vector
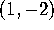 .
.
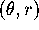 ? Test your conjecture by applying the
matrix
? Test your conjecture by applying the
matrix 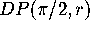 to the vectors
to the vectors 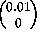 and
and 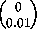 for
for 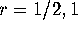 , and 2.
, and 2.
 -plane whose image under P is a
heart-shaped curve (with two cusp points).
-plane whose image under P is a
heart-shaped curve (with two cusp points).
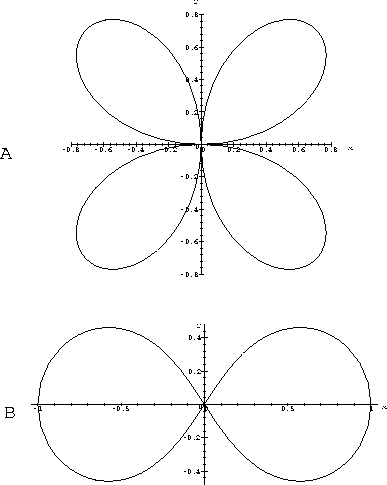
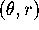 -plane.
-plane.