
You will have one week to complete this lab, professionally write up the answers, and submit it for a grade. There is also an exam next week, so do not wait until the last minute to complete the lab! (Hint: only two of the questions below require the use of the computer; you are encouraged to do some/all of the other questions before coming to lab!)
The purpose of the lab is
Background: A linear (harmonic) oscillator may be modeled by the differential equation

Here 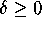 is a parameter called the coefficient of damping.
It reflects the amount of dissipation in the oscillator (think
``spring-mass system''). If
is a parameter called the coefficient of damping.
It reflects the amount of dissipation in the oscillator (think
``spring-mass system''). If 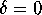 , then there is no friction; if
, then there is no friction; if
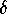 is large, then trajectories are quickly pulled into a sink
(meaning that the motion stops). The parameter
is large, then trajectories are quickly pulled into a sink
(meaning that the motion stops). The parameter  reflects a
constant external force that affects the system. For example, the
spring-mass system may be affected by gravity,
or the mass may be a piece of metal in a constant magnetic field.
reflects a
constant external force that affects the system. For example, the
spring-mass system may be affected by gravity,
or the mass may be a piece of metal in a constant magnetic field.
Set the parameters to 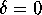 and
and 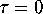 .
.
The period of an oscillation is the time that it takes for the position and velocity to return to their initial values. This corresponds to the time it takes for a trajectory in phase space to make a closed path. For our current values of the parameters, the amplitude of a trajectory is the largest value of x that the trajectory passes through. This will always occur when v=0.
Fix v=0 and let 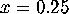 . The amplitude for this trajectory will be
. The amplitude for this trajectory will be
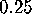 (why?), but what is the period? We can estimate the period
numerically by generating a trajectory, graphing
(why?), but what is the period? We can estimate the period
numerically by generating a trajectory, graphing 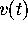 versus t,
and estimating the time that it takes for the oscillator to return to
v=0.
versus t,
and estimating the time that it takes for the oscillator to return to
v=0.
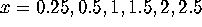 .
.
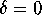 and
and
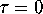 by computing the general solution,
by computing the general solution, 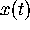 , of the linear
oscillator. (Hint: recall that the period of
, of the linear
oscillator. (Hint: recall that the period of 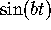 is
is 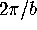 .)
How does the period change as you change the initial condition?
.)
How does the period change as you change the initial condition?
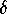 , the mass still oscillates (note
that the position alternates between positive and negative values). What is
the critical value of the damping at which the system changes from
being a focus to being a node? (Hint: use the ``pitchfork diagram.'')
, the mass still oscillates (note
that the position alternates between positive and negative values). What is
the critical value of the damping at which the system changes from
being a focus to being a node? (Hint: use the ``pitchfork diagram.'')
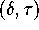 -plane that corresponds to the parameter values
that separate node equilibria from focus equilibria. This curve is
called a bifurcation curve in which eigenvalues of the
linearization change from being real to being complex.
-plane that corresponds to the parameter values
that separate node equilibria from focus equilibria. This curve is
called a bifurcation curve in which eigenvalues of the
linearization change from being real to being complex.
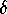 parameter is large, then the oscillator doesn't
oscillate much. We say that the system is overdamped. One application
for having a spring-mass system with large damping is a screened-door on a
porch. Why is overdamping desirable in this scenario? Can you think of
another application for an overdamped oscillator?
parameter is large, then the oscillator doesn't
oscillate much. We say that the system is overdamped. One application
for having a spring-mass system with large damping is a screened-door on a
porch. Why is overdamping desirable in this scenario? Can you think of
another application for an overdamped oscillator?
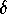 and
and  .
.
 (forcing) affect the location of
equilibria? Does this make sense physically?
(forcing) affect the location of
equilibria? Does this make sense physically?
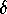 affect the location of
equilibria? Justify your answer (in words) by discussing a physical
oscillator.
affect the location of
equilibria? Justify your answer (in words) by discussing a physical
oscillator.
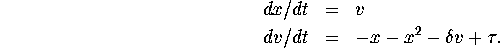

Figure: Bifurcation curves for a linear and
nonlinear oscillator.