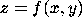 on a
domain in the plane:
on a
domain in the plane:
contourplot(f(x,y),x=a..b,y=c..d);For example,
contourplot(-x^4+2*x^2-y^2,x=-1.6..1.6,y=-1.6..1.6);
It is sometimes useful to tack an option like contours=40
onto the end of the contourplot command.
Note that smoother curves can be obtained by including a specification
for the grid parameter of the form
contourplot(f(x,y),x=a..b,y=c..d,grid=[k,k]);where k is an integer. The default value of k is 25.
Notice that a contour plot is a three dimensional plot of the level curves of the function viewed from above. You can see this by rotating the plot as you did with 3D graphics.
densityplot(f(x,y),x=a..b,y=c..d);In contrast with the contour plot, the density plot in Maple is a 2D object and cannot be rotated in space. For example,
densityplot(-x^4+ 2*x^2-y^2,x=-1.6..1.6,y=-1.6..1.6);
Plot1 := plot(cos(x),x=-Pi..Pi, color=red): #Note the suppressed output
Plot2 := plot(1 - x,x=-Pi..Pi, color=green):
display({Plot1, Plot2});
gradplot(f(x,y), x=a..b,y=c..d);For example, the gradient vector field corresponding to the function
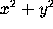 is a vector field in which all vectors point radially
outward from the origin:
is a vector field in which all vectors point radially
outward from the origin:
gradplot(x^2+y^2, x=-1..1,y=-1..1);
fieldplot([f1(x,y),f2(x,y)], x=a..b,y=c..d);For example, the vector field corresponding to the differential equation for a simple harmonic oscillator is plotted by
fieldplot([y,-x], x=-1..1,y=-1..1);