
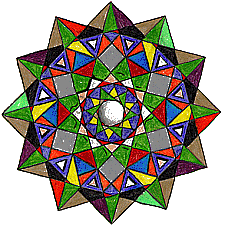


Symmetry has been catagorized to help us study it. As we look for patterns, we will also learn the language of symmetry. Here are a few definitions to start with. Don't worry too much about them now, but they are here for reference, and will make more sense later.
A transformation is an operation which maps, or moves, a figure to a new position... We will be looking at several transformations.
An isometry is a transformation which preserves lengths. That is a figure is moved, turned, and/or fliped, but it still is the same size and shape. All transformations we will be working with are isometries.
An image has Reflectional Symmetry if there is at least one line which splits the image in half so that one side is the mirror image of the other. Reflectional symmetry is also called line symmetry or mirror symmetry because there is a line in the figure where a mirror could be placed, and the figure would look the same. A reflection is sometimes called a FLIP.
An image has Rotational Symmetry if there is a center point where an object is turned a certain number of degrees and still look the same. A rotation is sometimes called a TURN.
An image has Translational Symmetry if it can be divided by straight lines into a sequence of identical figures. Translational symmetry results from moving a figure a certain distance in a certain direction also called translating (moving) by a vector (length and direction). A translation is sometimes called a SLIDE.
Extensions:
Java Activities
Next: Reflectional Symmetry