Complex numbers show up in a variety of interesting, real-world applications, such as the analysis of electronic circuits, high-speed flow over a jet plane, and so on. They are also heart and soul of certain fractals, such as that recently-discovered, four-dimensional object of nature represented by the union of the Mandelbrot and Julia sets.
This site introduces the basic idea behind complex numbers: where do they come from, how does one add them and so on? If you are already familiar with complex numbers, you may wish to skip ahead to those sections you would like to brush up on:
In mathematics, as in life, we often run up against a wall where something just seems impossible or unreal. In mathematics, however, working with the "unreal" often produces very real results. Complex numbers are an excellent example of this phenomenon.
The square root of negative one seems impossible, unreal. But it is actually very real, and a crucially important number in mathematics. So, we give it a name: i.
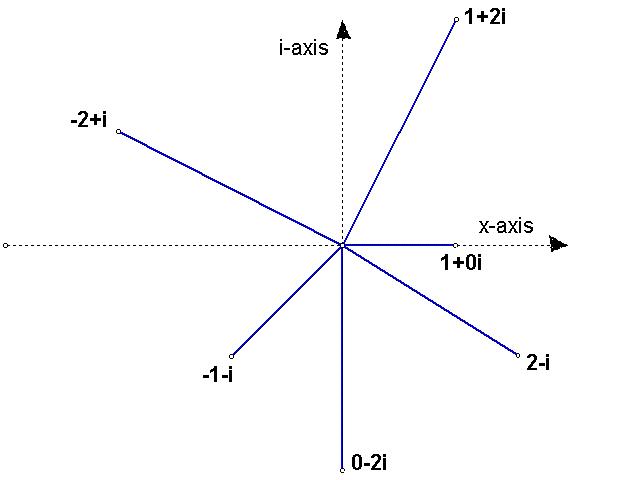
Graphing complex
numbers is done in a manner very similar to plotting a point (x, y) in
rectangular coordinates; the main difference is that the Y-axis now represents
IMAGINARY numbers, rather than the REALS, as when plotting points in rectangular
coordinates. Below is a graph demonstrating some numbers (points)
in the complex plane:

Incidentally, from this figure we can define the amplitude (or norm) and the
modulus of a complex number.
The amplitude is the length of the "arrow" or line which connects the
complex nummber to the origin.
The amplitude of 1+2i, for example, is (by the Pythagorean Theorem)
the square root of 12 + 22, which is the
sqaure root of five.
The modulus is the angle that the "arrow makes" when measured from the
x-axis;
1+0i, for example, has a modulus of zero degrees, and -1-i has a modulus
of 135 degrees.
You can find these angles using the trigonometric identity that
theta = inverse tangent of (i-component) over (x-component) - more examples
can be found in the last section on finding the nth roots of any number.
Forward
Backward
Back to Beginning
Back to Definitions Page
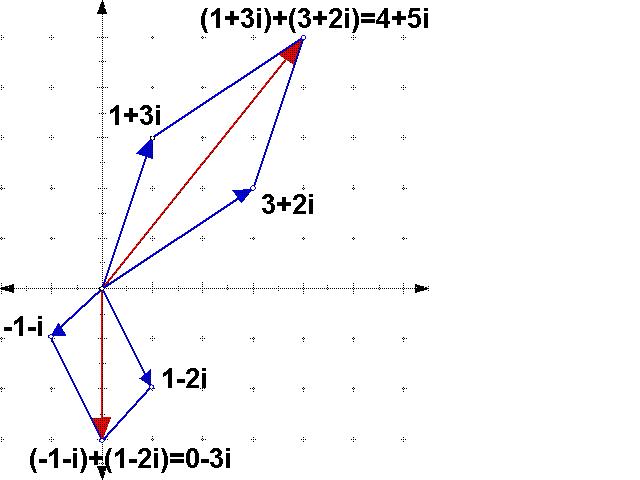
You add complex numbers by adding the real parts and then adding the imaginary parts. Examples:
Here's how that looks in the complex plane:
Forward
Backward
Back to Beginning
Back to Definitions Page
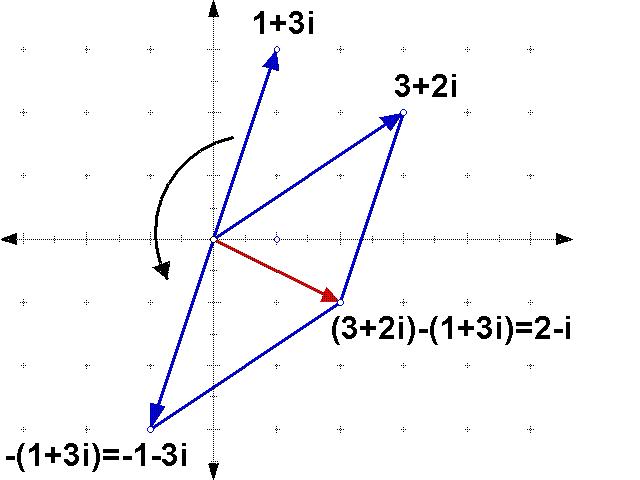
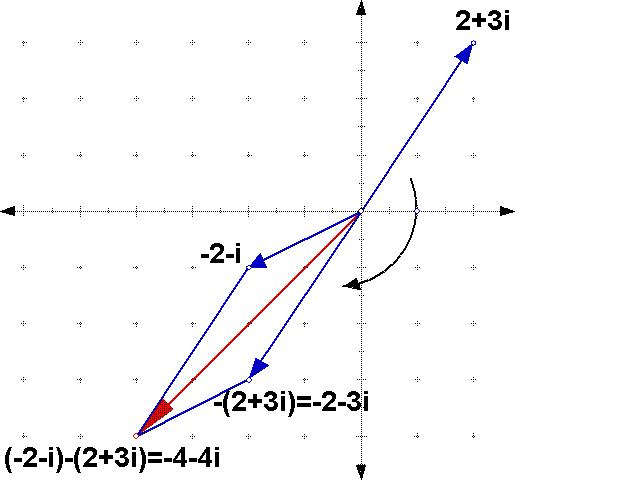
A To subtract complex numbers, we subtract the real parts and the imaginary parts. Examples:
Here's how that looks in the complex plane - note that it's the same as adding, except first we have to turn around backwards the "arrow" that we're subtracting:
Well, there's an algebraic way to do this and a pictorial way to do this. The algebraic method uses the good old "FOIL" method (multiply the first terms, then the outer terms, then the inner terms, then the last terms). B The key is to remember that i2=-1. Examples:
Showing what happens in the complex plane is rather more work, but I'm sure you'll agree that the beauty of it is definitely worth the effort!
Basically, it involves three steps:
Now, as Bill Nye would say, isn't that wild? Let's do an example. Let's show that:
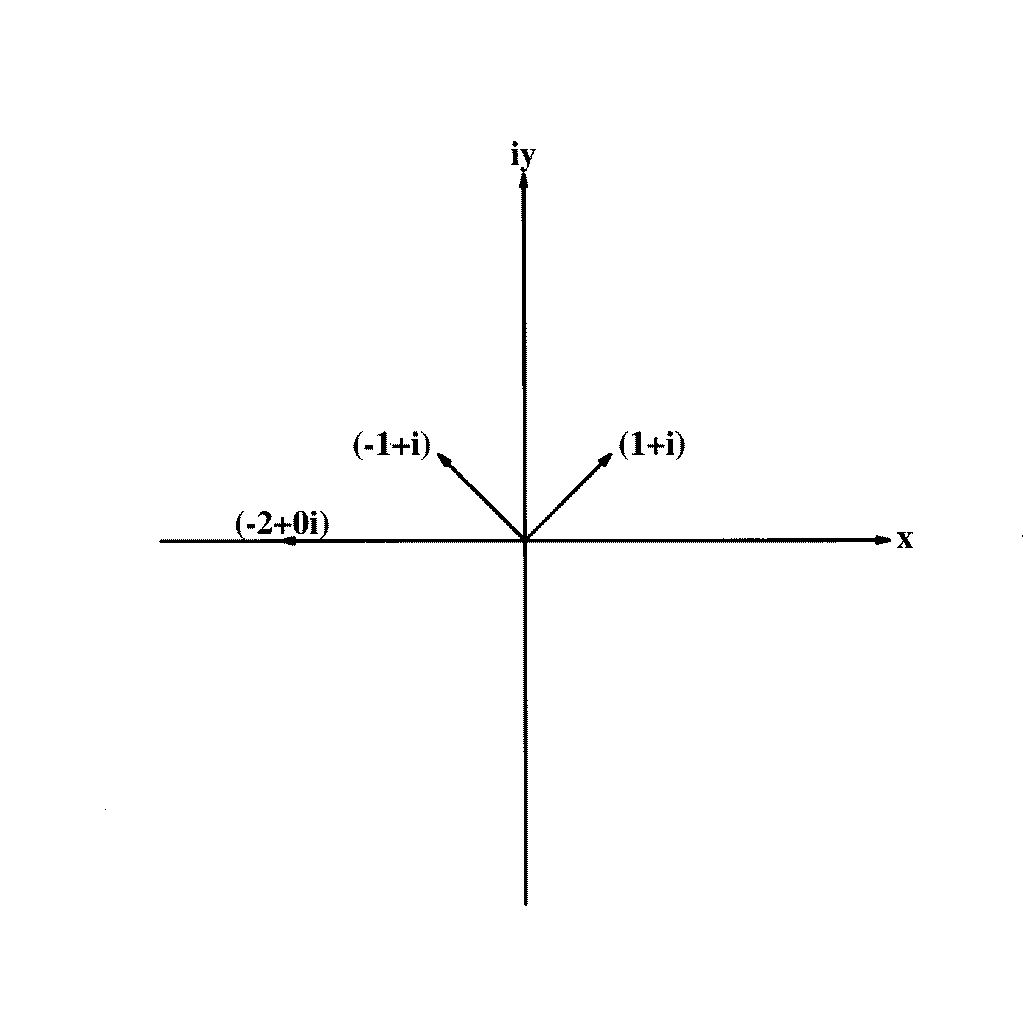
Here's the step-by-step:
So what we have here is a stretching of the arrows
and a rotation in the complex plane. Neat, eh?
By the way, notice that we've just verified
graphically the result we got earlier using the
FOIL method!
A
Forward
Backward
Back to Beginning
Back to Definitions Page
We'll be really brief and to the point here. Let's say you have z = 5+2i
and you want to find z2.
Remember how exponents work?
The superscript of two tells you to multiply z by itself two times.
So, you need to multiply (5+2i)*(5+2i).
Refer to the previous section on multiplying complex numbers if you're not
sure how to do that; if you try it yourself you should be able to verify that
the answer is 25 + 20i + 4i2 = 21 + 20i.
Forward
Backward
Back to Beginning
Back to Definitions Page
First of all, here's a nifty rule of thumb you can remember for all time: No matter what number you're talking about, if you're taking it's nth root, there are n of them! That means every number has two square roots, three cube roots, ninety-seven ninety-seventh roots, and so on. No matter what.
Ok, so how do we go about finding those roots? Again, it's a three-step process. See if this makes sense to you:
To show you how this works, five rather nipziffic examples have been worked out. First, the square roots of four are shown below. After taking a gander at those, there are four A more examples you can click on and check out - but before you do, you may want to have a little fun and see if you can work them out in your mind (or even on paper) before you actually look at the "answers"!