WELCOME TO THE FIFTH ROOTS OF (15+15i)!

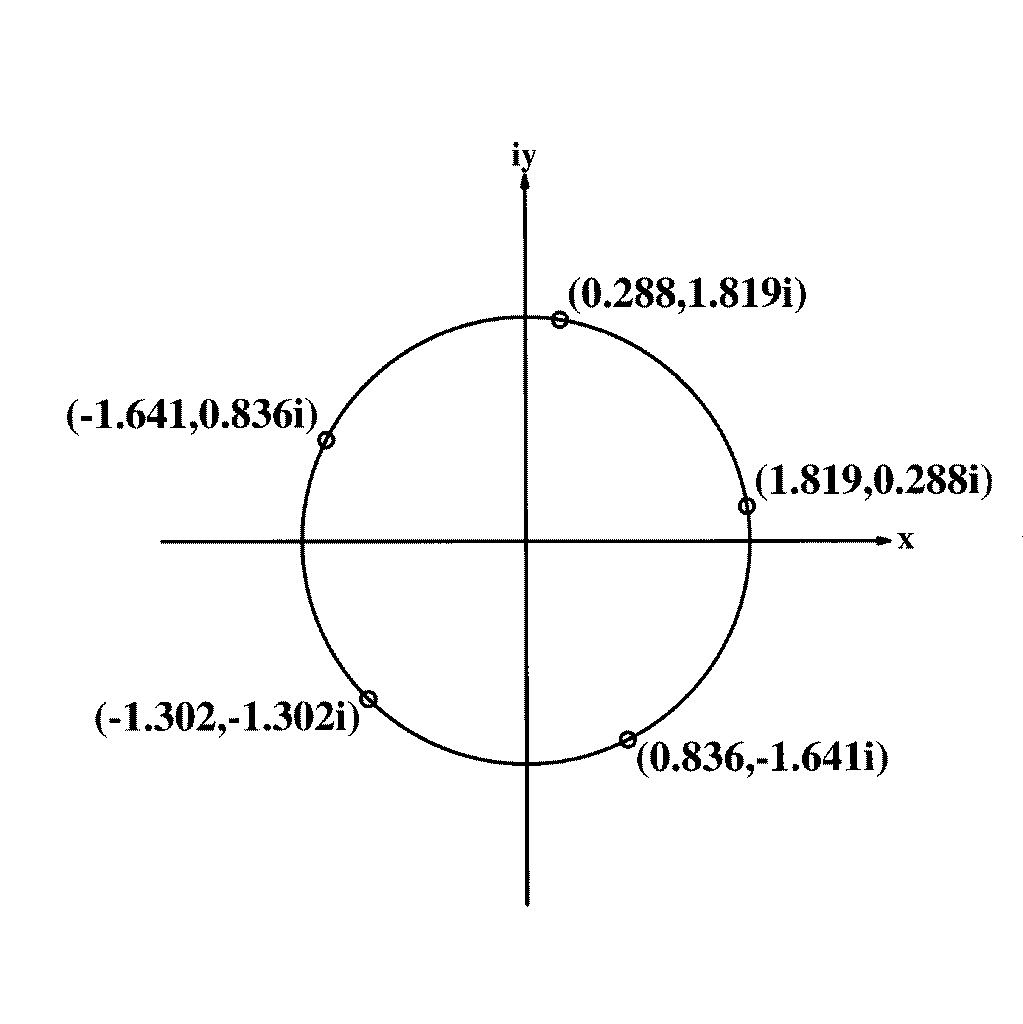
HERE'S HOW YOU FIND THEM:

(15+15i) has length (magnitude) (15^2+15^2)^1/2 = 21.213 and an angle to the x-axis, or modulus, of tan^-1 15/15 = 45 degrees;
so the root circle has radius 21.213^1/5 = 1.842,
the first root is at theta1 = 45/5 = 9 degrees,
and the remaining roots are at theta = 9 + n*360/5 = 81, 153, 225, and 297 degrees.