By George, it's Hamiltonian!

In the following problems you will show that the phase space vector field

F(x,v)=(dx/dt, dv/dt)=(v,-grad f(x))

for this system actually is Hamiltonian.

Question #3:

In the previous lab you showed that gradient vector fields have the property that work done in the field in getting between two points is independent of the path you take. Show that F(x,v) is not a gradient vector field by showing that it does not have this path-independent property. To do this, find two paths between points (0,0) and (0,3) such that the line integrals for work along each have different values.

One way to do this is to find parametrizations for your two curves and evaluate the line integrals

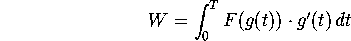
explicitly. We've provided some hints to do this with Maple.

Alternatively, you can give a proof without having to calculate integrals explicitly by carefully choosing the two paths based on how the geometry of the curves relative to the vector field affects the work integrals.

If you use the first method, show all your calculations and parametrizations. If you use the second method, give the geometric reasoning for choosing the curves you did. In either case, sketch your paths on the vector field plot.

Question #4:

There are plenty of vector fields that are neither gradient nor Hamiltonian, so your above results are not enough to show that F is Hamiltonian.

Show that F is indeed Hamiltonian by finding a function H(x,v) such that
dH/dx = -dv/dt
dH/dv = dx/dt.
Generalize this result for the one-dimensional gradient motion due to an arbitrary differentiable potential function f(x). Show that the equations of motion for such a system are
dx/dt=v
dv/dt=-grad f(x).
Then show that the system is Hamiltonian by finding the Hamiltonian H(x,v) generating this vector field.

Question #5:

One feature of Hamiltonian systems is that the trajectories of the vector field lie on the level sets of the Hamiltonian H(x,v).

For each of the initial conditions below, use the phaseportrait command to plot the corresponding trajectory of the vector field F.
- x(0)=0, v(0)=1
- x(0)=1, v(0)=3
Recall that the syntax for phaseportrait is
phaseportrait([v, -grad f(x)], [x,v], 0..7, {[0,a,b]},arrows=SLIM, stepsize=.1);
where a should be replaced by x0 and b should be replaced by v0.
Use the plot3d to plot the graph of H(x,v) for x=-7..7, v=-3..3. Determine the height of the level curve of H on which each of the above trajectories lie. Approximately sketch the trajectories on the graph of H at the correct height.

Next: Hamiltonian systems and energy
Previous: One-Dimensional Gradient Motion
Up: Introduction

Bob Thurman;thurman@geom.umn.edu>

Last modified: Tue Apr 2 13:48:52 1996