Hamiltonian systems and energy.
The vector field you have generated for this lab should
look familiar to you. We saw in a previous lab that it is the
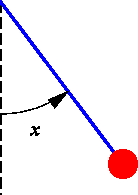
phase space vector field for a simple, undamped pendulum, where
x represents the angular displacement of the bob from its
rest equilibrium.
In physics we often describe the dynamics of a moving body in terms of
two types of energy -- potential and kinetic. The kinetic energy of a
particle of mass m moving with velocity v is defined
to be 1/2 mv^2.
Question #6:
- Use your answers to Question #4 to show that we can interpret the
Hamiltonian H(x,v) for the gradient motion due to a
one-dimensional potential function as "kinetic plus potential."
- Consider the phase space trajectories for pendulum motion that you
plotted in Question #5. Pick several representative points along each
curve, and discuss how the potential and kinetic
energies change between points. Analyze these changes in
terms of what is happening physically to the pendulum. For example,
is the potential energy ever 0 along the trajectory? Where is the
pendulum bob at those points?
- Explain what the phrase "total energy is conserved in Hamiltonian
systems" means.
Previous: By George, it's Hamiltonian!
Up: Introduction
Bob Thurman;thurman@geom.umn.edu>
Last modified: Tue Apr 2 13:49:18 1996

