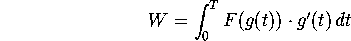The Definition of Work

with(plots): with(linalg):

In previous labs we defined a two-dimensional gravitational potential by:

Recall that F=-grad(P) is a (gradient) vector field representing the gravitational force felt by a particle at point (x,y).

Notice that if a satellite starts close to the sun and we want to move it farther away from the sun, then we must expend energy (probably in the form of burning rocket fuel). We might expect that the amount of energy we expend depends on the path that we use to to move the satellite.

We say that the work done by F in moving the satellite from (x0,y0) along the path parameterized by g(t), 0< t < T is given by:

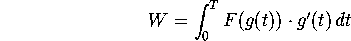
where g(0)=(x0,y0)and g(T)=(x1,y1). The work done by us against F is -W.

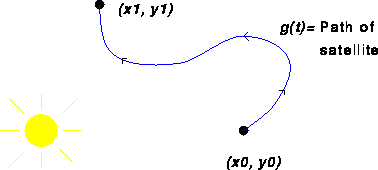
Figure 1

Question #1

• What does F(g(t)) represent?
• What does g'(t) represent?
• What does the dot product of F(g(t)) and g'(t) represent?

Question #2

1. Sketch the path.
2. Compute the work done (that is, energy expended) against the gravitational field in moving the satellite along the path for t=0..1.

• g(t) = [6+t,0]
• g(t) = [6*cos(2*Pi*t),6*sin(2*Pi*t)]
• g(t) = [t+6*cos(2*Pi*t),6*sin(2*Pi*t)]