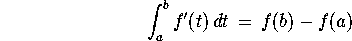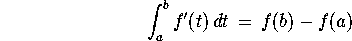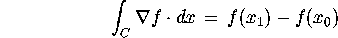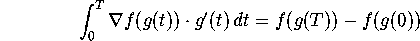The Gradient Theorem
The fundamental theorem of calculus relates the integral of a
derivative to the value of a function at endpoints of an interval.
Specifically, if f is a differentiable function of one variable
on the interval [a,b], then:
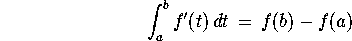
The gradient theorm says something very similar for functions of several
variables. Specifically, if C is a piecewise-smooth curve connecting x0
to x1, and if grad(f) is a continuous vector
field, then:
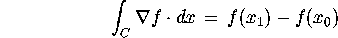
or, if we parameterize C by g(t), where g(0)=x0 and
g(T)=x1 then
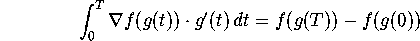
Question #3
Verify the gradient theorem for the previous problem, by computing the
right-hand side for each g. (Hint: First decide what f is
in this problem.)
Question #4
In this simplified model of the Solar System,
- How much work is done by sending a probe from earth to
somewhere else (say, Jupiter) and then
back home? Explain your answer and explain why you don't need to
know the "halfway point."
- How much work is done in one year as the earth undergoes one orbit around
the sun?
Next: Equipotentials
Up: Introduction
Previous: The Definition of Work
Frederick J. Wicklin <fjw@geom.umn.edu>
Bob Thurman <thurman@geom.umn.edu>
Document Created: Mon Jan 9 1995
Last modified: Tue Mar 26 09:03:58 1996