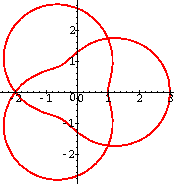Tying the Knot
Consider the planar curve parametrized by
t -> ( cos(2t)(2+cos(3t)), sin(2t)(2+cos(3t)) )
This curve is the projection onto the (x,y)-plane of
a knot. A knot is a closed curve in
three space. We say that a knot is "knotted" if it cannot be
untwisted into a copy of a circle. The circle is called the "un-knot."
You can visualize parametrized knots using Maple's spacecurve
command.
Question #7
Determine how to parametrize a "knotted knot" so that the projection of
the knot onto the (x,y)-plane is the curve given above.
How can you show that your parametrized curve is knotted?
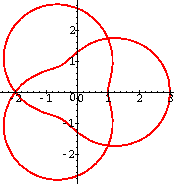
The planar projection of a knot.
Up: Introduction
Previous: Moving on to 3D
Frederick J. Wicklin <fjw@geom.umn.edu>
Jeremy Case
Document Created: Mon Feb 20
Last modified: Tue Feb 27 08:46:39 1996