Inscribed Angle Conjecture

Activity Sheet

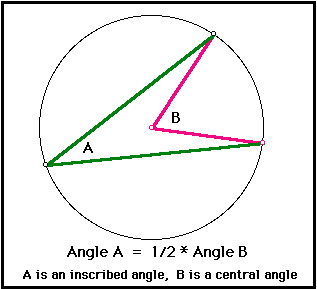
The objectives for this activity sheet are:

1. To determine your understanding of the Inscribed Angle Conjecture. Typical geometric problems requiring the ideas of this conjecture, coupled with ideas from previous conjectures, are given for you to solve.

2. To give you the opportunity to explore this conjecture further through construction activities involving:
   
   • Geometer's Sketch Pad
   • Compass and Straight Edge

Directions: Open the Geometer's Sketch Pad program on your computer. Then follow these directions:

1. Start by constructing any circle

2. Create an inscribed angle by constructing two chords with a common endpoint

3. Construct the central angle which has the same intercepted arc as your inscribed angle.

   
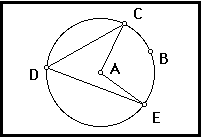
   (Your sketch should look like this: labels for the points might differ)

4. Measure both the inscribed angle, the central angle, and the Arc Measure. Record each of these values.
   • Angle CDE = ??
   • Angle CAE = ??
   • Arc CBE = ??

   Do your measurements support what is claimed in the conjecture?

5. Use the mouse to drag any of the points to change the shape of the picture. Note the relationship between the measures of the central and inscribed angles as you move the points. Hopefully, the central angle is twice as big as the inscribed angle.

   Is this the case?

1. Use a compass to construct a circle on your paper. Carefully mark the center of this circle.

2. With a straight edge, construct an inscribed angle by constructing two chords with a common endpoint.

3. With your straight edge, construct the central angle with the same intercepted arc as your inscribed angle. (Your construction should look like the figure above.)

4. Use a protractor to measure the inscribed and central angles. Record these results.

   Inscribed angle = ???
   Central angle = ???

5. What is the relationship between these two measurements?

6. If you did not find that the central angle is twice as big as the inscribed angle, what do you think caused this?

7. Try another construction, using a different circle, and repeat the measurements of inscribed and central angles.
8. Do these results support the conjecture? If not, what happened?

1. A = 40
2. B = 35
3. C = 30
4. D = 80
5. E = 40
6. F = 50
7. G = 50
8. H = 86
9. J = 34
10. L = 17
11. M = 103
12. N = 17
13. P = 140
14. Q = 100
15. R = 30
16. S = 60