Vertical Angles Conjecture

Activity Sheet

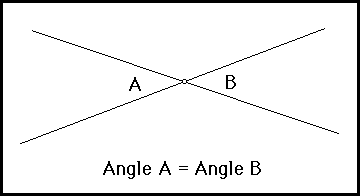
The objectives for this activity sheet are:

1. To determine your understanding of the Vertical Angles Conjecture. Typical geometric problems requiring the ideas of this conjecture are given for you to solve.

2. To give you the opportunity to explore this conjecture further through construction activities involving:
   
   • Geometer's Sketch Pad
   • Compass and Straight Edge

Directions: Open the Geometer's Sketch Pad program on your computer. Then follow these directions:

1. Construct two lines which meet at a single point. Lines AB and CD.
2. Construct a point at the intersection of these two lines. Give this point the label "E".
   
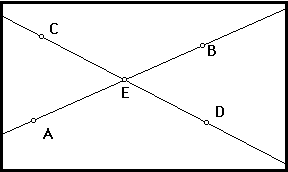
   (Your sketch should look like this.)

3. Measure the angles AEC and BED by selecting the points and using the Measure Menu.
4. Compare the two measurements. What do you find?
5. Drag the points A, B, C, and D to see what happens to the angle measurements.
6. Do the same for the angles AED and BEC. What happens?

1. Use a straight edge to construct a pair of intersecting lines.
2. Label the lines AB and CD, and the intersection point as E (see diagram above)
3. Use a protractor to measure pairs of vertical angles.
   For example, measure the angles AEC and BED. What happens?
4. Do the same measurements for angles AED and BEC. What happens?
5. Construct other pairs of intersecting lines to determine if this conjecture always holds.
6. What happens?

1. x = 35
2. y = 55
3. z = 90