Slope Procedure

1. Choose two points on the line. If it is a segment, choose the endpoints.
2. Start with the left point.
3. Since the formula is m= rise/run, we do the "rise" first since it is in the numerator (the top part of the fraction). You either rise up or rise down. SO, count how many spaces it takes to up (or down) to get to the second point.
4. If you "rise up", the number is positive; if you "rise down", the number is negative.
5. Now, you ALWAYS "run over"! If you follow the procedure correctly, you will always run over to the right. Count how many spaces it takes to go "run over" to the second point.
6. Take the numbers you have and put in in the rise/run formula. YOU NOW HAVE THE SLOPE!
7. Check to see if you have the positive or negative sign correct. If the line is uphill, it will have a positive slope. If it is downhill, it will have a negative slope.

Let's look at an example.

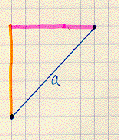
Look at line segment a. Start with the left point. The orange segment is the "rise". Since you "rise up" to go to the second point, it will be positive. When you count the spaces, you must go up 5 spaces. Therefore, the rise is +5. Now we are ready to "run over". You have to run over 6 spaces to get to the second point. Therefore, the run is 6. Since the slope m= rise/run, the slope of segment a is +5/6. Since it is going uphill, we know we have the +/- sign correct!