
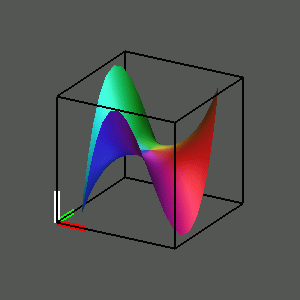
We can change the exponent and observe the graphs of other complex functions, for example w = z^3.

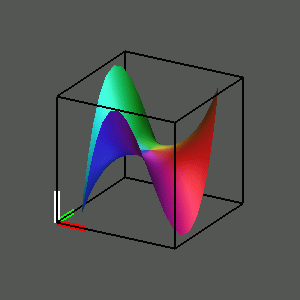
To observe this, play the movie
Similarly we can rotate from the graph of the cubing function to the graph of the cube root relation z = w^1/3. In the case of the real cubing function, there was an inverse function since every real number has a unique real cube root. On the other hand, every complex number other than zero has three distinct cube roots.


To observe this, play the movie
We summarize this investigation of the graph of the complex cube (and its inverse, the complex cube root), by situating the four images at the vertices of a diagram, with arrows between certain vertices. Selecting any vertex plays a movie of a rotation of that object in three- space, and selecting an arrow plays the rotation in four-space from one view to the other.
There are two interesting transformations directly from the domain of the cubing function to the range of that function. To see them, select one of the arrows below.