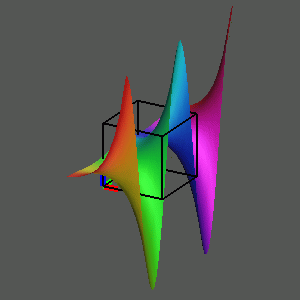
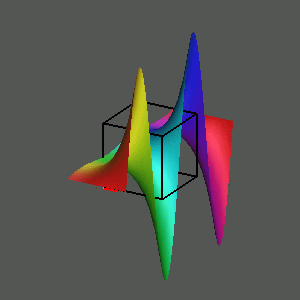
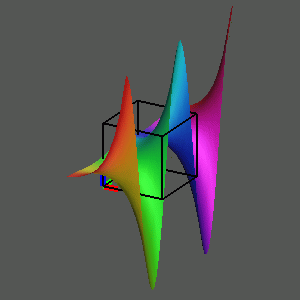
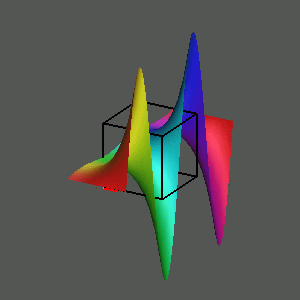
To observe this, play the movie
The inverse relation, the complex logarithm, has a quite complicated Riemann surface, with a real part that is a surface of revolution of the graph of the exponential function in the plane and an imaginary part that is a right helicoid, resembling a circular staircase.
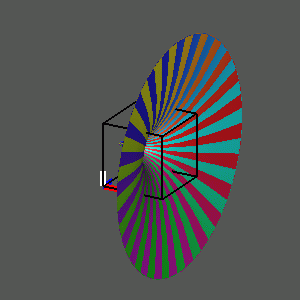
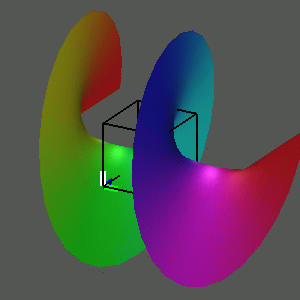
To observe this, play the movie
We summarize this investigation of the graph of the complex cube (and its inverse, the complex cube root), by situating the four images at the vertices of a diagram, with arrows between certain vertices. Selecting any vertex plays a movie of a rotation of that object in three- space, and selecting an arrow plays the rotation in four-space from one view to the other.