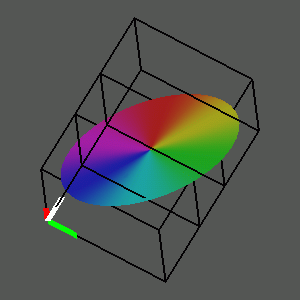
For example, the graph of the identity function restricted to the unit disc |z|<=1 inscribed in the previously considered square will be an ellipse inscribed in the parallelogram that is the graph of the identity function on that square.

We can now observe the graph of the squaring function where the domain is restricted to the unit disc. When we look at the graph itself, we display the domain in the (x,y) plane and watch as we move from the real to the imaginary part of the squaring function. Effectively we are projecting into three-space the locus (x, y, cos(a) u + sin(a) v) as the angle a goes from 0 to pi/2, where the points (x, y) are restricted to lie in the unit disc x^2 + y^2 <= 1.
To observe this, play the movie. In the film, we make a complete rotation of 2pi to return to the starting position, then continue on for an additional pi/2 to arrive at the final destination.
Just as in the case of functions of a real variable, we can rotate the graph of a complex function to exhibit the graph of its inverse relation. In the case of the squaring function, this leads to a graph of the square root relation z = w^1/2, a complicated surface in three-space that appears to intersect itself.
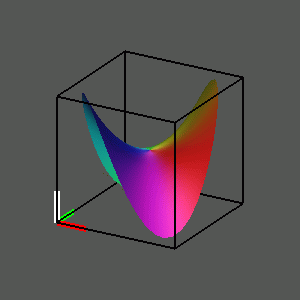
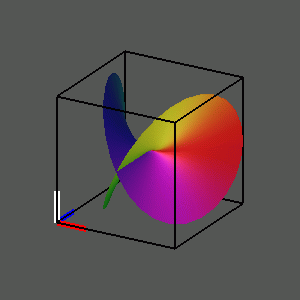
To observe the effect of rotating from the imaginary part of the squaring function to the real part of the square root, play the movie
We can now rotate in four-space to move from the real part of the square root (x, u, v) to the imaginary part (y, u, v). Effectively we are projecting into three-space the locus (cos(a) x + sin(a) y, u, v) as the angle a changes from 0 to pi/2. The picture we see was first described in the last century by the mathematician Bernhard Riemann, and it is known today as the Riemann Surface of the Square Root.


To observe this, play the movie
We summarize this investigation of the graph of the complex square (and its inverse, the complex square root), by situating the four images at the vertices of a diagram, with arrows between certain vertices. Selecting any vertex plays a movie of a rotation of that object in three- space, and selecting an arrow plays the rotation in four-space from one view to the other.
There are two interesting transformations directly from the domain of the squaring function to the range of that function. To see them, select one of the arrows below.