One of the most powerful uses of visualization in the early part of a course in functions of two or more variables is in the study of partial derivatives. Students learn that the critical points of a function occur where both the partial with respect to x and the partial with respect to y are zero, but all too often this fact is merely an algebraic statement. It can have a strong visual aspect if we use information about the partial derivatives to color the function graph.

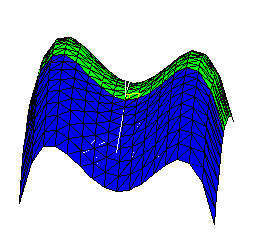
We can illustrate the geometric content of this concept by shining a bright light from the right along the x-axis and coloring the points of the graph depending on whether they are illuminated or in shadow (more precisely, according to the algebraic sign of the derivative with respect to x.) The boundary line between the two colors corresponds to those points with tangent planes perpendicular to the yz-plane.
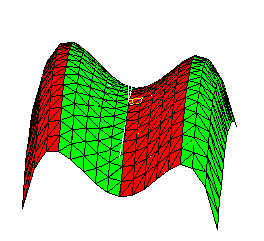
Similarly we may color the points of the graph by the sign of the partial derivative with respect to y, reflecting the illumination of the graph by a bright light from the far north. The boundary line between two different colors in this case indicates points with tangent planes perpendicular to the xz-plane.
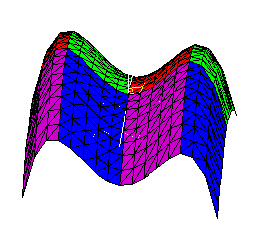
If we color using both lights simultaneously, then the intersection of the boundaries between colors corresponds to points where four different colors come together, and the tangent plane is simultaneously perpendicular to the yz- and xz-planes, therefore to the z-axis. Thus we have a geometric way of identifying the critical points of the graph of a smooth function, where the tangent plane is horizontal.