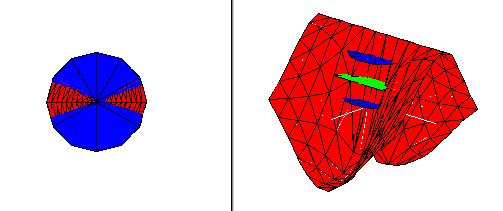
In order to appreciate the definiton of continuity for functions of two variables, it is important for students to understand how an epsilon challenge can be met with a delta response, no matter how small the positive epsilon is that has been put forth.

This process is illustrated in the following interactive demonstration, where one student chooses an epsilon so small that the graph of the function over a disc neighborhood of a point is not contained between the planes over the point at distance epsilon above and below the value of the function at the point.
But the second student can choose a delta radius small enough that the graph over this restricted disc domain does fit between the planes.
Each subsequent epsilon challenge can also be met by a choice of delta, so the function is continuous at the point in question.
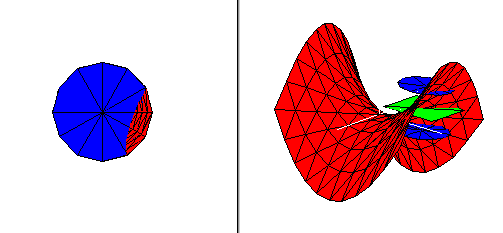
The above example is the graph of f(x,y) = x**2 - y**2, and it is continuous at all points. If we use the same techniques to examine the graph of the function f(x,y) = (x**2 - y**2)/(x**2 + y**2) for (x,y) not equal to (0,0) and f(0,0) = 0, we find that the epsilon challeng cannot be met, even for epsilon as large as 1/2. No matter how small a delta we choose, the graph of the function above the delta disc around the origin has points lying above the plane at height 1/2. The function is not continuous at the origin.