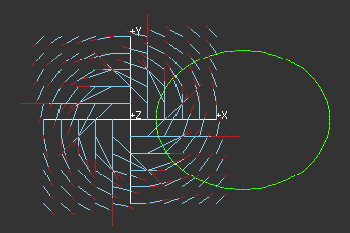
Line integrals over a closed curve in the plane can be visualized as
ordinary integrals with respect to the arclength parameter. We
illustrate this by considering a famous integrand, [-y,x]/(x**2+y**2)
defined at all points except the origin. When the
ellipse does not surround the origin, the value of the line integral
is zero. Note that there are two points of the ellipse where the field
is perpendicular to the tangent line of the curve. Near the origin,
the effect of the vector field is a negative number with large
absolute value, while far away from the origin, the effect is small
and positive. The total effect is zero.

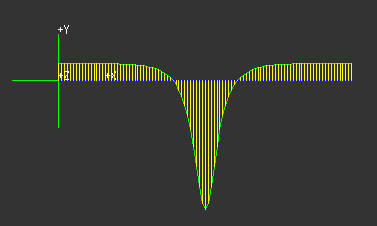
When the ellipse surrounds the origin, the total value of the integral is 2 pi. In this case, the integrand in the line integral is positive at all points. The effect is greater for points closer to the origin. By changing the position of the center of the ellipse, the student can observe the changeover that takes place when the ellipse passes through the singularity of the vector field at the origin.

