The Number Bracelets Game

Contents.

Introduction and rules.

This is a game that lots of kids are playing (or so I've heard). You only need to be able to add whole numbers to play it, but there are interesting variations and extensions for people who like to think about mathematical patterns (6th graders, high school students, math majors, graduate students, ...)

The origin of this game, in this form, is an activity by Marilyn Burns (About Teaching Mathematics, a K-8 Resource, Math Solutions Publications, 1992.) Another version can be found in Joan Cotter's book of Math Card Games.

Imagine that you have lots of beads, numbered from 0 through 9, as many as you want of each kind.

Here are the rules for making a number bracelet:

Example.

Choose 2 and 6 for the first and second beads:
.
The third bead is 2 + 6 = 8 :

To get the fourth bead, add 6 and 8, then use only the ones digit: 6 + 8 = 14; use 4:

8 + 4 = 12; use 2:

4 + 2 = 6:

But the last two beads are the same as the first two, so instead of making a long string, use 2, 6, 8, and 4 in a loop, or bracelet.

Another example.

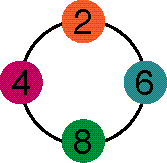
Choose 1 and 3 for the first and second beads:
.
The third bead is 1 + 3 = 4 :

3 + 4 = 7:

4 + 7 = 11; use 1:

7 + 1 = 8:

1 + 8 = 9:

8 + 9 = 17; use 7:

9 + 7 = 16; use 6:

7 + 6 = 13; use 3:

6 + 3 = 9:

3 + 9 = 12; use 2:

9 + 2 = 11; use 1:

2 + 1 = 3:

But the last two beads are the same as the first two, so pop them off and make a bracelet:

Questions

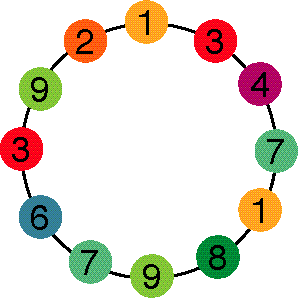
Think about these before looking at the answers. Some of the questions are easier to answer if you work with other people and make lots of different bracelets.
To Extensions and generalizations.

To:
Susan Addington's Home Page at the Geometry Center || Susan Addington's Home Page at Cal State San Bernardino