Number Bracelets Answer 1

How long (or short) a number bracelet can you make?

I'm going to call the length of the bracelet the number of times you have to add to get back to the first bead. This is the same as the number of beads, except in one case:
The shortest bracelet has length 1 and starts with (0,0). If you add one time, you get back to the first 0. But the bracelet has two beads. (Every bracelet has to have at least two beads to start.)

The next shortest bracelet starts with (0,5), and has length 3:
0 5 5

There is a bracelet of length 4 that starts with (2,6) (the first example on the main page):
2 6 8 4

There is a bracelet of length 12 that starts with (1,3) (the second example on the main page):
1 3 4 7 1 8 9 7 6 3 9 2

There is a bracelet of length 20 that starts with (0,4)
0 4 4 8 2 0 2 2 4 6 0 6 6 2 8 0 8 8 6 4

There is a bracelet of length 60 that starts with (0,1)
(I'll let you have the fun of writing all the beads.)

How many different starting pairs of beads are there?

There are 10 choices for the first bead:
0 1 2 3 4 5 6 7 8 9
For each of these choices there are the same 10 choices for the second bead. For example, if the first bead is 0, the possibilities for the first two beads are
(0,0) (0,1) (0,2) (0,3) (0,4) (0,5) (0,6) (0,7) (0,8) (0,9) [10 choices]
So there are 10 x 10 = 100 pairs in all.

The order of the numbers is important, so we have to count ordered pairs: pairs of numbers in a particular order. In mathematics, ordered pairs are written in parentheses with a comma in between: (2,6).

How many different number bracelets are there?

Note that if you start on an already-made bracelet at some other pair of beads (in the same direction as the original bracelet) you get the same bracelet by adding. For example, (6,8) is a pair of beads on the (2,6) bracelet. By adding you get
6 8 4 2,
which, if written in a circle, is the same as the (2,6) bracelet:
2 6 8 4

A bracelet of length L has L different starting pairs on it. For example, the (2,6) bracelet has the starting pairs (2,6), (6,8), (8,4), and (4,2)
on it. If a starting pair occurs twice in the same bracelet, then you made a mistake: the pattern would repeat exactly the same after the second repeat of the pair as after the first repeat. So you can't actually have the same pair twice in the same bracelet.

There are 100 different starting pairs (see above). The bracelets listed at the top of this page have lengths
1, 3, 4, 12, 20, and 60,
so they account for
1 + 3 + 4 + 12 + 20 + 60 = 100
pairs, so we have found all the bracelets.

Will a number bracelet always loop back to the beginning, or can you have a string of beads that never repeats?

Because there are only 100 different starting pairs (see above), you would run out of pairs after a necklace of length 100 and have to repeat. In fact, the longest you can go is only 60.

But could it loop back to another pair in the bracelet, without ever returning to the original pair?

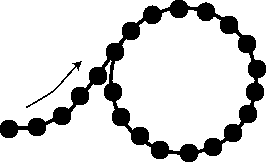
There is a rule for going backwards on the bracelet. (Can you discover the rule?) If the bracelet looked like the picture above, there would be two rules at the branch point, one for each branch, and no way to choose which rule to use. So this can't happen, because there is a single rule for going backwards.

If you start with the same two beads, but in the opposite order, do you get the same bracelet? Do you get the same bracelet in reverse?

You don't generally get the same bracelet, even reversed, because the fourth number is the sum of the second and the third. The starting pair in reverse gives a fourth number which is the sum of the first and the third of the original bracelet.

Example: The (2,6) bracelet has length 4. But the (6,2) bracelet is the same as the (0,4) bracelet, which has length 20.

Back to main page.