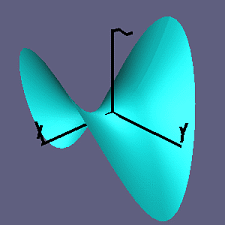
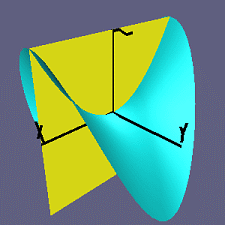
To study the curvature of S at p, we slice S by planes containing n and consider the curvature of the resulting curves.
Example: Let S the graph z=f(x,y) where f(x,y) = x^2-y^2 (the Saddle) and let p the point (0,0,0).
Slicing the surface with a plane:


Movie showing different resulting curves when we rotate the plane by pi:
The curvatures of these resulting curves are called normal curvatures at p.
The maximum normal curvature k1 and the minimum normal curvature k2 are called principal curvatures.
In the movie, k1 is the curvature of the red curve and k2 is the curvature of the blue curve.
 The Geometry Center Home Page
The Geometry Center Home Page
 Topological Zoo
Welcome Page
Topological Zoo
Welcome Page
Comments to: webmaster@www.geom.uiuc.edu
Created: April 9 1995 ----
Last modified: Sun Apr 28 16:09:52 1996
Copyright © 1995 by
The Geometry Center,
all rights reserved