Equations for the Pseudosphere

The parametric equations for the pseudosphere are:

f(u, v) = ( cos(u)sin(v), sin(u)sin(v), cos(v) + log(tan(v/2))),

0 <= u <= 2*pi, 0 < v < pi.

Notice that when v goes to zero and to pi, the z coordinate of the pseudosphere goes to negative infinity and to positive infinity respectively. In the picture, b <= v <= pi-b , where b is chosen arbitrarily. This parameter "b" cuts off the peaks of the pseudosphere.

With this parameterization we got:

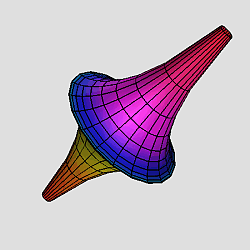
Notice that the mesh is compressed in the middle, therefore we did a reparameterization in order to get a more uniform mesh.

The new parameterization is:

d = atan(-a) + pi/2 

w = atan(2a*v/pi - a) + pi/2 

v1 = (pi-2b)(w-d)/(pi-2d) + b 

f(u,v1) = ( cos(u)sin(v1), sin(u)sin(v1), cos(v1) + log(tan(v1/2)))

Where "a" controls how much the mesh is compressed or stretched.

After this parameterization we got:

Up: The Pseudosphere

The Geometry Center Home Page

Topological Zoo Welcome Page