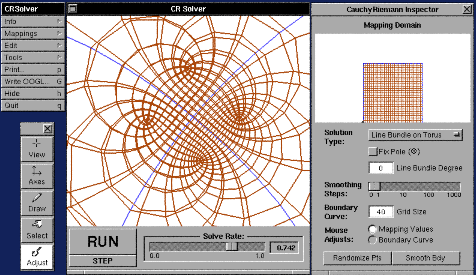
CRSolver accomplishes this through an iterative process, which starts with an initial guess for the map, and then repeatedly applies a relaxation step to make the map more and more conformal. Here is CRSolver in action:

Mapmakers have to contend with an insoluble problem: how to portray the round earth on a flat map. There is no way to do this without introducing some kind of inaccuracy. Some choice must be made about which features to portray accurately, and which features to accept some distortions in. Mathematics tells us what choices are available.
One choice that is possible is to correctly portray all angles, but allow distances to be distorted. This means that small shapes will be drawn accurately, even though the scale on the map may change drastically from one point to another. A map which correctly portrays angles like this is called a conformal map. A familiar example is the Mercator projection.
CRSolver finds conformal maps, but of rectangles or parallelograms rather than of spheres. It displays the results by showing how a regular grid of `longitude' and `latitude' lines on the rectangle or parallelogram would appear in the map.
Holomorphic and meromorphic maps.
The mathematical equations that determine when a single-layer map is conformal--the Cauchy-Riemann equations--admit more general solutions when the map is allowed to superimpose multiple layers. Each layer must still be conformal, of course, but branch points may now appear, where the different layers join together and intermingle. Multi-layered conformal maps with branch points are called holomorphic.
In addition to branch points, we may wish to allow some points to be mapped to infinity; such points are called poles of the map (the Mercator projection, for example, maps the usual North and South Poles to infinity). Multi-layered conformal maps with poles and branch points are called meromorphic.
Holomorphic and meromorphic maps play a central role in the mathematical field of complex analysis.
For further info...
For further information consult the online help pages that come with the CRSolver program. Bug reports should be submitted by email to burchard@geom.umn.edu.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: May 15 1994 ---
Last modified: Jun 18 1996