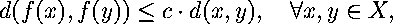
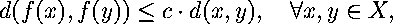
for some real constant 0<= c <1, the contractivity factor.
Theorem: (The Contraction Mapping Theorem) Let f:X->X be a contraction mapping on a complete metric space (X,d). Then f has exactly one fixed point, a, in X, and:
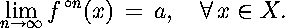
Contraction mappings are the elementary building blocks of IFSs, but they are un-interesting by themselves (as seen by the above theorem).
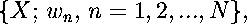
where each wn is a contraction mapping. We define the contractivity factor of the system to be:
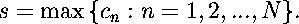
Here cn is the contraction factor for wn.
Def: Given a metric space (X,d), we define another metric space (H(X),h(d)). Where H(X) is the set of all nonempty compact subsets of X, and h(d) is the Hausdorf distance between two elements of H(X). In rough terms, the Hausdorff distance between two sets A and B is d if every point of A is within d of some point of B and vice versa.
This metric space (H,h) is in some sense the natural space in which fractals live. In a general way a fractal is an element of this space. However, this is a mathematical abstraction of our intuitive ideas about what a fractal should be (since H includes lot's of normal geometric objects as well.)
Theorem: Let {X; wn, n=1,2,...,N} be a hyperbolic iterated function system on the metric space (X,d) with contractivity factor s. Then the map W:H(X)->H(X) defined by:
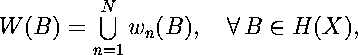
where
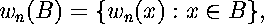
is a contraction mapping on (H(X),h(d)) with contractivity factor s. Further, the unique fixed point, A, of W is given by:
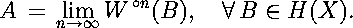
Note that a point of H is actually a non-empty compact set of the original space X. This set A is called the attractor of the IFS.
It is the attractors of IFSs, which live in H(X), which are really fractals. Indeed, almost all of the well known fractals, as well as many less well known ones, are the attractors of appropriate IFSs. See some examples generated using Fractalina.
Below is an applet that implements the deterministic algorithm for the IFS:
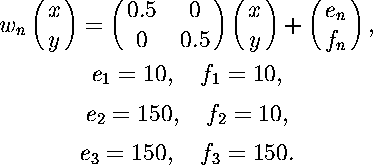
Notice that the initial set can vary widely, but the result converges rapidly to the attractor of the IFS. (The attractor of this IFS is the well known Sierpinski triangle.)
To chose the initial set drag in the window, then use the Iterate button to
step through iterations on that set.
This theorem provides the mathematical basis for animations of IFSs (in particular for Franimate!). The effect implied here has been called "blowing in the wind", because an imaginary fractal tree can be made to blow in an imaginary mathematical breeze, by continuously varying a parameter to the IFS of the "tree".
Fractals Everywhere, Michael Barnsley, Academic Press Inc., 1988.
 IFSoft Home Page
IFSoft Home Page![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
This page was created by Noah
Goodman.
Comments to:
webmaster@www.geom.uiuc.edu
Created: Sep 23 1996 ---
Last modified: Tue Oct 8 11:30:11 1996