MODULE: Monge's Theorem.

Part 4: Dilations.

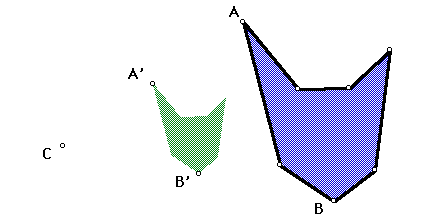
We would like to present a different view of the construction of Monge's Theorem. This involves the use of "dilations", that is, transformations of the plane that are either contractions or expansions about a point (the "center of the dilation"), by a constant ratio. If this ratio is smaller than one, the dilation is a contraction. If larger than one, an expansion.

Construct a point C in the plane, and mark it as the center of the dilation. Now draw any polygonal figure, and dilate it about the center C by a fixed ratio (1/2, or 3, or whatever). Drag around this polygon, and observe how the image changes. In particular look at the vertices, their images and the center. Can you see any relation among them?

We look now at the converse problem. That is, if we are given a figure and its image under a dilation, can we find the dilation?

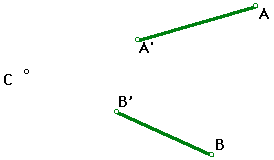
Suppose you have a point A, and its image A' under a certain (unknown) dilation. Where would the center of the dilation have to be? Is there only one possibility? Construct two points, and then find several dilations (that is, combinations of centers and ratios) giving the second point as image of the first one. (It is convenient here to use dilations by a "marked ratio". Once we pick the center, what would this ratio be?)

What if now we have two points and their images? Assuming the points and the images are not on one line, How can you find the center? What can you use as a ratio? We saw that just one image does not completely determine the dilation. Can you give the two images arbitrarily, and still get a dilation?

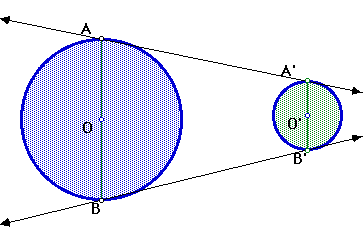
Returning to the Monge theme, start now with two circles of different radii. Is there a dilation so that the image of one of the circles is the other one? Where is the center? Can you construct it? Does the figure look familiar? Check that the dilation really maps one circle onto the other.

Now let's look at what happens when we "compose" two dilations, i.e., what happens if we follow a dilation by another one.

Draw two points, C1 and C2, to be used as centers. Draw a figure to dilate. Mark C1 as center, and dilate the figure by some fixed ratio. Now mark C2 as center, and dilate the figure resulting from the first dilation about this center, by some other ratio. (Just be careful only that the product of the two ratios is not 1). Move the original figure around, and see how does the final image change. Again, it is convenient to restrict your attention to only a pair of vertices. What relation does the final image seem to have with the original figure? If it were a dilation, how would you find the center? Do you see any relation between the two original centers and this new one?

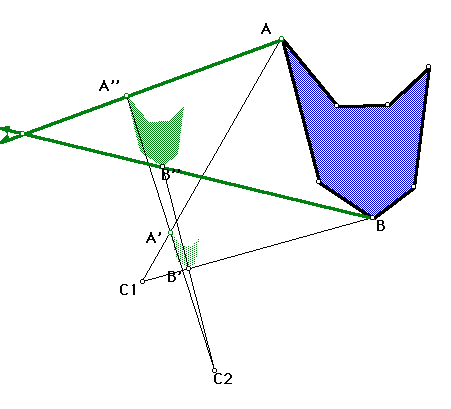
Repeat the above construction, but now with the product of the ratios equal to 1. What happens now with the final figure? What with the "new center"? Can you guess what is the relation between the original and the final image? Check whether you are right or not .

On why the new center is where it is: As before, construct two points C1 and C2 to be used as centers of dilations. Now construct the line given by them, and construct a point P on it. Look at what happens to this point under the two successive dilations. Where is the first image going to be? What about the final one? Consider now the original point P and its final image: where should the center of the composition be, then?

These last observations have in them all the ingredients necessary for showing why Monge's theorem is true.

How can you describe the Center of Symmetry of two circles in terms of dilations?

Consider now the set-up of Monge's Theorem: Three circles of different radii. How can you describe a Center of Symmetry, using dilations, in terms of the other two?

What does Monge's Theorem say about these dilations? Is it true?

The Geometry Center Home Page

Author: Eduardo Tabacman, revised and edited by Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996