Next: Circles and tangents
Up: Table of Contents

MODULE: Monge's Theorem.

Part 0: Introduction.

Consider any three circles on the plane, no two of them of the same radius. Pick a pair, and draw the lines that are tangent to both of them, externally. (There are two kind of common tangent lines: if both circles lie on the same side of the tangent line, it is an "external" tangent; otherwise the tangent is "internal").

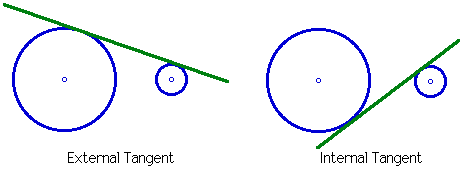
Since the radii of these two circles are different, these tangent lines are not parallel; they must then intersect at a point P1. If we repeat this with the two other possible pair of circles, we get two more pairs of external tangent lines.

Sketch (as accurately as you can) the drawing described above; Monge's Theorem gives a general result about this drawing. Try to guess what the result might be.

We will work towards constructing the drawing you just made using Geometer's Sketchpad, a computer program for exploration of plane geometry. Along the way, we will see that to be able to construct the figures, we will have to use the software to explore their geometric properties. We will see how the software can be used as a tool for discovery; you will be able to make a more informed guess as to the conclusion of Monge's Theorem. Finally, once you discover the conclusion, we will explore why Monge's Theorem is true, using some geometric transformations.

Next: Circles and tangents
Up: Table of Contents
[HOME] The Geometry Center Home Page

Author: Eduardo Tabacman, revised and edited by Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996