Peaucellier's Linkage Homework

Peaucellier's linkage questions


1. Turn in the following Sketchpad materials:
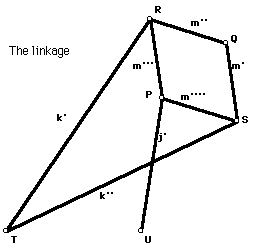
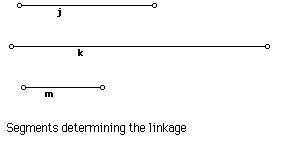
   1. Sketch and script for Peaucellier's linkage.
   2. Script for inversion of a point.
   3. Constructed inverse of a circle through the center of the circle of inversion (the center of the circle of inversion was called A in the lab).
   4. Constructed inverse of a line not through the center of the circle of inversion (the center of the circle of inversion was called A in the lab).
   5. Constructed circle of inversion for the linkage.
   6. Constructed shape traced by the point Q in the picture of the linkage above (this is the same picture as in the lab).

2. Answer questions in Part 2B. Give brief justifications of your answers using the definition.

3. Fill out the table in Part 2C.

4. Part 2D: Explain how to construct the inverse of a circle c which goes through the center of the circle of inversion. Make sure that your construction works with a circle of any radius. In other words, it should not rely on intersection between the circle c and the circle of inversion.

5. Part 2D: Explain how to construct the inverse of a line not through the center of the circle of inversion.

6. Part 3A #3: Using the definition of inversion, how can you verify that P and Q are related by inversion? (P and Q are shown in the picture from the lab shown above) What is the center of the circle of inversion?

7. Part 3B: What is the radius of the circle of inversion in terms of j, k, and m? Explain how you can use segments of lengths j, k, and m to construct a segment of the length of the radius. (Again, j, k, and m are labelled above.)

   ---

   General Sketchpad questions on inversion.

   It is assumed that you are familiar with Sketchpad. Thus, the following questions do not give step by step help on the technique of creating a sketch.

8. Investigate what happens to angles under inversion as follows:

   

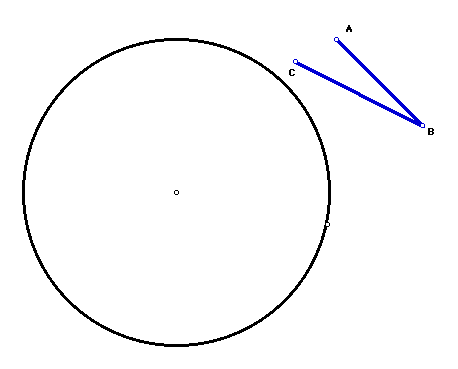
   Start with an angle determined by three points A, B, and C, and two segments AB and BC, shown in the above figure. Construct a circle of inversion with center not collinear with AB or BC. Invert the points and segments through this circle. Remember that the line segments will invert to curved arcs.

   

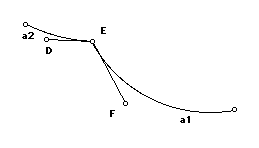
   The angle between two arcs meeting at a point is the angle formed by their tangent lines at that point. This is illustrated in the above figure. Using this, measure the original angle and the new angle, and compare your answers. Your answer to this problem should reference a Sketchpad sketch.

   

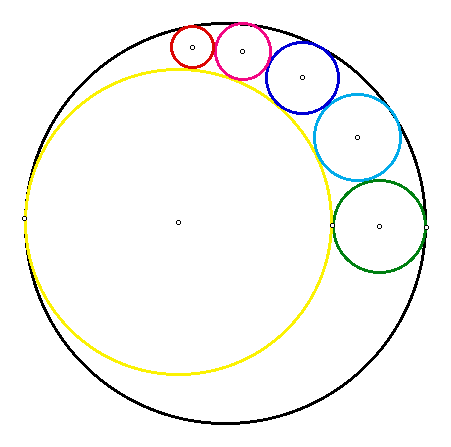
   In this problem you create the first four circles in the picture shown above. Starting with three tangent circles, two inside of the third, here is a method of constructing a circle tangent to all three circles. See the two figures below. Repeating this process gives the beautiful picture of arbelos, known to the ancient Greeks.

   

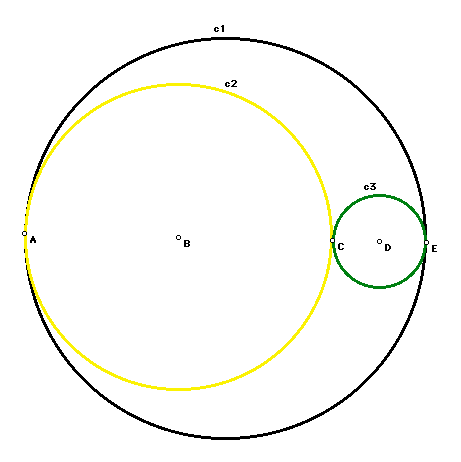
   Referring to the labels in the figure, create a circle c5 with center A, as shown in the figure below. Invert circles c1,c2, and c3 through circle c5. What do you get? Relate this to the chart you made for the lab.

   

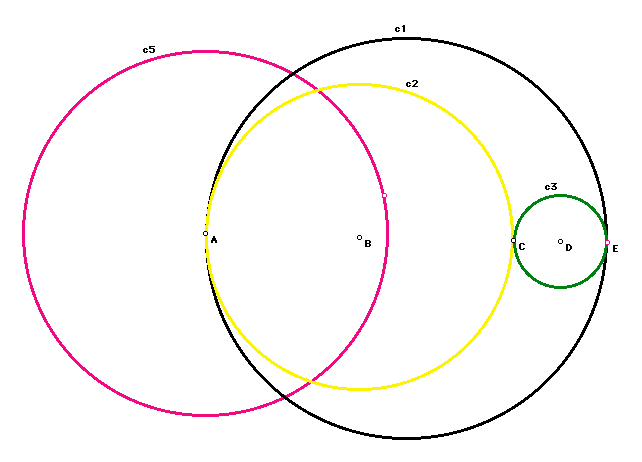
   Create circle c6 tangent to the three inverses. Notice that by inverting, you made it possible to do this construction.

   Using your answer from the previous problem justify this statement: inversion preserves tangency. Using this information, create circle c4, tangent to c1, c2, and c3. This is the first step in constructing the arbelos picture. For extra credit, create two more circles in the arbelos picture.

   See Dan Pedoe, Geometry, A Comprehensive Course page 89 for more information.

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jun 11 1996