Sketchpad Homework

1. Work through the first part of Jim King's notes on Sketchpad. The more you do, the easier you will find the labs using Sketchpad. At the very least, learn to do all of the items on the following list of basic Sketchpad commands:
   1. Construct points, segments, lines, circles.
   2. Label an object. Change the name of the object.
      Note that in the labs and homework, you will want to change the name of your objects to match the names given in the writeup.
   3. Construct a segment, line, or ray through two specified points.
   4. Construct a circle given its center and a point on it. Construct a circle given its center and radius.
   5. Construct the intersection of two objects.
   6. Trace the locus of an object.
   7. Construct the midpoint of a segment.
   8. Given a line j and a point A, construct lines perpendicular and parallel to j through A.
   9. Make and save a Script.
   10. Translate, rotate, and dilate. Specifically, given a segment AB, find a point C such that AC = .3 (AB) such as in the following picture:

       

       In addition, construct two segments, mark the ratio between their lengths, and dilate by marked ratio.

   11. Save a Sketch.
   12. Hide an object. This is never explicitly mentioned in the homework, but if the sketch becomes too complicated, you may wish to hide objects to make it simpler. In particular, do not delete objects used in defining other objects. Only hide them.

   ---

   The following questions are designed to give a general familiarity with Sketchpad. They can be done at any time in relationship to the Sketchpad labs.

2. Any three noncollinear points lie on a circle. In this exercise, you will use Sketchpad to construct the circle through three points. Turn in the sketches described below as "sketch1" and "sketch2." "sketch2" is the completed picture. Briefly summarize the mathematics justifying what you did to make the completed picture.
   1. Construct three noncollinear points. Use the Show Labels command on the Display menu so you can distinguish them. Save this as "sketch1".

      

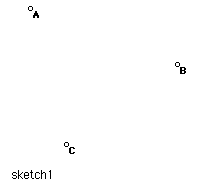
      Eventually, you will construct the circle through these points. However, first think about all circles passing through two points.

   2. Create a separate sketch ("sketch2") consisting of just two points, A and B. Where are the centers of circles through these two points?

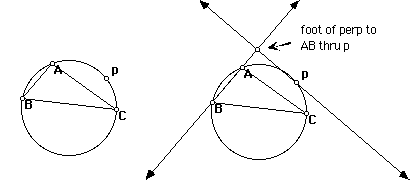
   3. Construct circles containing the two points A and B: Construct a line segment at the top of your sketch. This represents the radius of the circle containing A and B. Construct a circle with center A and radius given by the segment. Then construct a circle with center B and radius given by the segment. The intersection points of these two circles are possible centers of circles containing A and B with radius given by the segment. Think about why this is true. Are there any other circles with this radius that go through A and B? The intersections are at points F and G in the picture below. Now pick either F or G to be the center of a circle, and pick A to be a point on the circle. Notice that B is also on the circle. This supports the statement above about circles containing A and B.

      

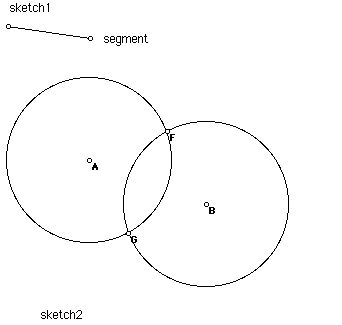
   4. Look at all the possible centers of circles through A and B. To do this, select the points F and G, and pick the Trace Locus command from the Display menu. Vary the length of the segment. What does the set of centers for circles through A and B look like? (Think about this before you look at the next part.)

   5. Construct this line of possible centers: make a segment with endpoints A and B. Construct the Point at Midpoint of the segment. Select the midpoint and segment, and construct the Perpendicular Line.

   6. You may want to find the perpendicular bisector of the segment between two points again. Make a script to do it in one of the following two ways:
      
      1. Select everything in the sketch. Select Make Script from the Work menu. Save the script.
      2. Start with two new points. Select New Script from the File menu. On the Script window, hit the record button. Do all the steps to create the perpendicular bisector. Hit the Stop button. Save the script. Select two new points, and try playing it back.

   7. Go back to sketch1. For each pair of points, there is a line of centers of circles through the pair of points. Construct these lines using your script.

   8. How do you know that the three lines intersect at a point? (State a theorem from geometry.) This intersection point is the center of the circle through the three points.

   9. Construct the circle through the three points.

3. Given two points A and B, what is the set of points P such that AP + BP = a constant K? ("AP" is my shorthand for "the distance from point A to point P." Also, K must be greater than the distance AB, or there are no points P.) In this exercise, you use Sketchpad to look at this set and formulate a conjecture about its shape. (Do you remember what the shape will be from previous geometry courses?)

   Turn in your final sketch. Briefly describe the mathematics of how you constructed it. Write your conjecture for the shape traced in part d. Answer the questions in part e.

   1. Construct two points A and B. Construct a segment CD at the top of your sketch. The distance CD is the constant K. Construct a point E on this segment CD.

   2. Notice that CE + ED = constant K. Use this to construct P as follows; construct the set of points distance CE from A. Construct the set of points distance ED from B.

      

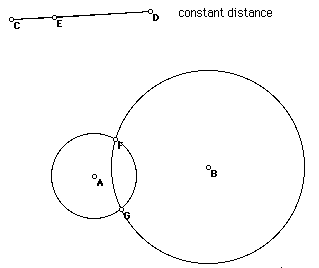
   3. The points of intersection of these two circles (F and G) have the property we wanted to study. Construct the points F and G, the intersection of the circles.

   4. Trace Locus of F and G as you vary E. What does this set look like?

   5. Experiment: move A and B around. Change the constant K (by moving D). Now trace the locus in part d again. How does the value of K effect the set of points you trace? What would happen if K were exactly distance AB?

   6. By now you should have a conjecture about the traced set. Can you prove your conjecture? Place the origin at the midpoint of the line segment between A and B. Write equations involving the coordinates for points in the traced set. Write an equation describing the shape that you conjecture. Are the these equivalent?

4. Given a point A and a line j, what is set of points P such that for some e< 1, PA = e Pj? (Pj is the distance from point P to line j.) In this exercise, you use Sketchpad to look at this set. Refer to the following picture.

   

   Turn in your final sketch. Briefly describe the mathematics of how you constructed it. Answer the questions in part f.

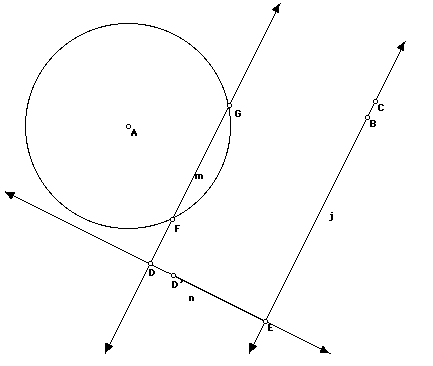
   1. Construct a point A and a line j.

   2. Construct a point D not on j. Construct a line m parallel to j through D.

   3. You need a segment that has length equal to the distance from j to m. Construct a line n perpendicular to j through D. Construct the E, the intersection point of n and j. The distance ED is the distance from j to m. Do you see why?

   4. You want a segment of length e times ED. Thus use dilation: choose E and D. In the Transform menu, select the Mark Vector command. Now use the Mark Center command, marking E as the center. Now use the dilate command. Dilate by fixed ratio e (the picture uses e=.8) to 1. This will give you a point D' such that ED' =e ED.

   5. Make a circle around A with radius given by ED'.

   6. Finally, the intersection F and G of the circle with line m is the set in question. Trace the locus of intersection points as you move D. What do you think this set is? How would the set change if you used a different number e?

5. A person is standing 9 feet up on a 12 foot ladder. The ladder slides down the wall. Assuming that the person stays at the same spot on the ladder, what is the path of the person as the ladder falls? Here is a picture of the situation. I have hidden some things, so don't just try to reproduce this picture.

   

   Turn in your final sketch. Briefly describe the mathematics of how you constructed it. Answer the question in part d.

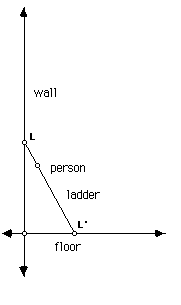
   1. Construct the line which is the wall. Construct a point on the wall. Construct the floor, a line perpendicular to the wall through the point. Construct another point L on the wall. This is the point the ladder hits the wall.

   2. Off to the side, draw a segment the length of the ladder. Use this segment and point L to construct the ladder. Hint: Remember that the ladder is a segment with one endpoint L. The ladder is always the same length. Its other endpoint L' is on the floor. Thus the other endpoint is on a circle with center L. What is the radius of the circle?

   3. Construct the person. Hint: the distance from L to the person is .25 times the distance LL'. Do you understand why?

   4. Trace the locus of the person as you move L. Does the set of traced points look like part of an object which is familiar to you? What do you suppose the shape would be?

6. Simpson's line: In an above question, you constructed a circle through three points, known as the circumcircle of the triangle formed by the three points. Connect these points to form a triangle. Pick a point p on the circumcircle; through p, construct the perpendiculars to the sides of your triangle. What can you say about the feet of these perpendiculars? This is called Simpson's line. (The foot of the perpendicular is the point at which the perpendicular line intersects the line containing the side of the triangle.) What happens when you trace Simpson's line as you vary p? Your writeup should reference a sketch. (Reference "A Little Geometry," Mathematica in Education, Vol.3, No.1, Winter, 1994.)

   

7. Pythagorean theorem. Use Sketchpad to illustrate the Pythagorean theorem. Your writeup should reference a sketch. You may need to include text for explanation.

8. Given any triangle consider the following configuration of the following nine points:
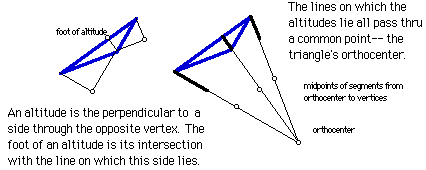
   the midpoints of the sides, the feet of the altitudes, and the midpoints of the segments joining the orthocenter to the vertices. Construct the points, guess on what curve the points lie and construct this curve. Test your conjecture by moving your original triangle around in a variety of ways.

   Your writeup should reference a sketch. For more information, consult the Penguin Dictionary of Curious and Interesting Geometry, by David Wells.

   

The Geometry Center Home Page

Author: Evelyn Sander
Comments to: webmaster@www.geom.uiuc.edu
Created: Jun 09 1996 --- Last modified: Jul 31 1996