a = r A
where A is the angular acceleration (i.e. the rate at which the angular velocity of the rod is changing) and a is the instantaneous linear acceleration the particle experiences out on the circle.
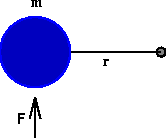
By Newton's second law for linear motion, if we apply a force F to the particle, then F = m a . On the other hand, since we have a rotating system, we would like to work with torque , instead of force, so we multiply both sides of the equation by r . Then
T = F r = m r a .
Finally, we use the equation derived about, to convert from linear acceleration to angular acceleration:
T = m r a = m r (A r ).
Rearranging terms gives the desired formula T = (m r 2) A.
Copyright © 1996 by The Geometry Center. Last modified: Fri Apr 12 15:52:12 1996