Next: Harvesting
Return to: Limits on Growth
Up: Outline
Equilibria, Stability, and Phase Space
We now know that we can find equilibria solutions to a differential
equation by finding values of the population for which
dP/dt=0. But we also observed that the two equilibria
solutions for the logistic population model differ: for one
equilibria, nearby trajectories (solutions to the
differential equation) are "attracted" to the equilibrium; for the
other equilibrium, nearby trajectories are "repelled." We call the
first case a stable equilibrium (also called a sink)
and we call the second case an unstable equilibrium
(also called a source).
In the real world, we will almost never observe an unstable
equilibrium solution. For example, if a ball is pushed down a hill as
in Figure 1, it may end up in the positions indicated by Q or
S, but it would be a lucky push indeed that results in the
ball being positioned exactly at R. For this problem, the
positions Q and S are stable equilibria for the
ball, whereas R is an unstable equilibrium. Even if we carefully place
the ball at point R, a gentle breeze or earth tremor
will cause the ball to move away from R. In contrast,
placing a ball at point Q or S will result in the
ball staying near that stable equilibrium, even on a gusty day.
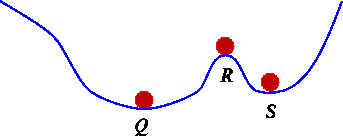
Figure 1: Equilibrium positions for a ball on uneven terrain.
Notice that geometrically, it is easy to tell the difference between the
stable and unstable equilibrium positions of the ball in Figure 1.
At the stable positions, the terrain is concave up, whereas at the unstable
equilibrium, the terrain is concave down. The next question asks you to
generalize this observation to the logistic model
dP/dt = k P - A P2.
Note that the right-hand side of the logistic equation is solely a function of
the current population P, so
let's define F(P) = k P - A P2.
As before, let's call the two solutions to F = 0
C and E, with C < E (See Figure 2).
We suspect from numerical experiments that C is an unstable
equilibrium. By definition, this means that if we choose an initial population to
be C + a where a > 0 is a small number (in particular,
a < E), then
we expect dP/dt evaluated at C + a to be positive.
Therefore the population will increase, thus driving it
away from C. This argument can be made rigorous by
substituting the value of C into F(C+a) and showing that
the resulting number is positive for all small values of a > 0.
We say that F defines a vector field on the phase
line. At each point where F > 0, we picture a small
vector pointing to the right (the positive P direction) based
at that point, and we let the length of the vector correspond to the
magnitude of F at that point. Similarly, at
each point where F < 0, we picture a
vector pointing to the left. At equilibria, we imagine the zero vector, since
the magnitude of F at equilibria is zero.
These vectors give us geometric intuition into the questions:
if a population is P, will the population increase or decrease?
Will it change quickly or slowly?
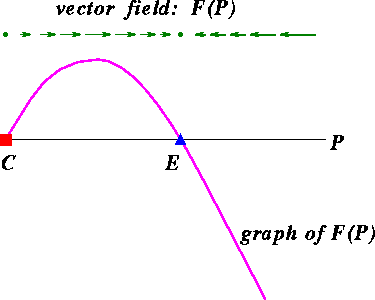
Figure 2: The vector field F(P) on the phase space
gives a geometric interpretation of how solutions to a differential equation evolve.
Question 6
- Construct an argument to verify that the equilibrium
E is a stable equilibrium. Note this time that
a may be either positive or negative.
- Geometrically describe and sketch what a vector field looks like
in the neighborhood of a sink. In the neighborhood of a source?
- How can you determine the stability of an equilibrium by
looking at the derivative (with respect to P)
of the vector field? Relate this
result to the physical interpretation of stability for a ball
on a hill (See Figure 1) based on the concavity of the terrain.
(Careful! Making the connection to a "second derivative of something"
is trickier than it looks. A hint is to think of the vector field as
giving a force, but Figure 1 shows the graph of
a so-called "potential". Start by sketching the "force field"
(also known as the vector field) for Figure 1.)
- You are modeling two different populations. The net birth rate and
coefficient of overcrowding for the second population is
exactly twice that of the first population.
Compare the location of equilibria and sketch the
vector fields for these model populations.
By looking at the vector fields can you determine which population is which?
Can you determine which population has the shorter expansion phase?
Question 7
We've been considering solutions to differential equations that
are functions of time. That means that we can also consider the solution to be
the parametrized path of a particle as it moves along the
phase line (the P-axis). Use the
Population Simulator to
generate trajectories of the logistic model and simultaneously display the
solutions on the phase line.
As you generate trajectories, vary the length of time over which you
follow the solution. Also vary the initial population, the growth
rate, and the coefficient of overcrowding. To help you track the
parametrized path corresponding to the last trajectory you generated,
only the last initial condition is used to plot the path of the
particle on the phase line. This path shows up in red.
- Based on your observations, what is the relationship between
the graph of the function P(t) and the
parameterized curve on the phase line that describes the same solution?
- A friend of yours who is not taking calculus looks over your shoulder
as you are doing this lab and asks you,
"How long will it take a population that does not start
at equilibrium to reach equilibrium." Craft a
response to this question that is accessible to someone who has not
had calculus.
Next: Harvesting
Return to: Limits on Growth
Up: Outline
The Geometry Center Calculus Development Team
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: May 15 1996 ---
Last modified: May 15 1996
Copyright © 1996 by
The Geometry Center
All rights reserved.



![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page