![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and ContentsThe standard approach for globalizing one-dimensional unstable manifolds is to start with a point on the linear approximation, take the line segment between this point and its f-image, and compute iterates of this (approximation of a) fundamental domain. For the two-dimensional version of this method, one would take a circle of points on the linear approximation. If the circle is close enough to H, one may assume that the f-image of this circle is almost a circle as well. Therefore, one obtains an annulus as a fundamental domain.
Since the fundamental domain cannot be iterated as a
continuous object, one needs to discretize it.
As was pointed out earlier, merely iterating the
points of the discretiation will lead to a possible accumulation of
points on a one-dimensional submanifold of
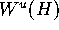 ; see also
Figure 2.
In our situation, we can avoid this accumulation by keeping track
of where the iterates of the circle intersect
; see also
Figure 2.
In our situation, we can avoid this accumulation by keeping track
of where the iterates of the circle intersect
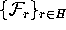 .
However, there is a second problem. Away from
H, the iterates of the initial circle on the linear approximation of
.
However, there is a second problem. Away from
H, the iterates of the initial circle on the linear approximation of
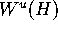 may not look like circles
at all. In practice, already after
a few iterations, the successive images of the fundamental domain
may have a very `unpractical' shape.
For example in the 3D-fattened Arnol
may not look like circles
at all. In practice, already after
a few iterations, the successive images of the fundamental domain
may have a very `unpractical' shape.
For example in the 3D-fattened Arnol d
family in Section 5.1, the invariant circle contains two
fixed points. Close to the one-dimensional stable manifold of the fixed
point that is repelling on H, the f-image of an annulus grows a
`nose' that stretches and winds around the circle
several times, but at least once. This is
unpractical, because it is unclear how one can obtain a nice mesh
on the unstable manifold in this situation. It may look like the
unstable manifold has holes.
d
family in Section 5.1, the invariant circle contains two
fixed points. Close to the one-dimensional stable manifold of the fixed
point that is repelling on H, the f-image of an annulus grows a
`nose' that stretches and winds around the circle
several times, but at least once. This is
unpractical, because it is unclear how one can obtain a nice mesh
on the unstable manifold in this situation. It may look like the
unstable manifold has holes.
In order to avoid such problems we drop the idea of iterating a
fundamental domain. Instead we let the manifold grow at the same speed
in each direction, which means that we
add rings of fixed width  . How this
can be done is explained in the following section.
. How this
can be done is explained in the following section.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:49:51 1997