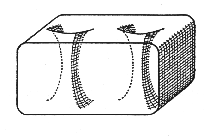
It is easy to find a tight sphere: the standard round sphere will do (in fact, any convex surface is a tight sphere; tightness is a generalization of convexity). A polyhedral example is the cube.
Given a tight surface, it is always possible to add a handle to the surface without losing tightness. Kuiper gave the following two-handled torus as an example of how to do this:

For the polyhedral case, we can describe this process in more detail. Take any two faces that are not co-planar, remove a triangle from the center of each (below, left), then add a triangular tube between these two holes (right).
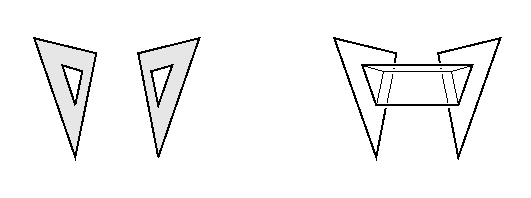
The resulting surface is still immersed (since the stars of the new
vertices are embedded
![[More]](pix/Link.gif) )
and tight (since the new vertices are not
extreme vertices
and the new handle does not change the convex envelope of the surface
)
and tight (since the new vertices are not
extreme vertices
and the new handle does not change the convex envelope of the surface
![[More]](pix/Link.gif) ).
).
Starting with a sphere (a cube, for example), and adding handles in this way, we can obtain a tight immersion for a torus of any genus, either smooth or polyhedral, so every orientable surface has a tight immersion.
![[Right]](pix/Right.gif) Non-orientable tight surfaces
Non-orientable tight surfaces
![[Up]](pix/Up.gif) Kuiper's initial question
Kuiper's initial question
7/20/94 dpvc@geom.umn.edu --
The Geometry Center