Next: 9.4 Relations between Cartesian, Cylindrical, and
Spherical Coordinates
Up: 9 Coordinate Systems in Space
Previous: 9.2 Cylindrical Coordinates in Space
To define spherical coordinates, we take an axis (the polar
axis) and a perpendicular plane (the equatorial plane), on which
we choose a ray (the initial ray) originating at the intersection
of the plane and the axis (the origin O). The coordinates of a
point P are: the distance 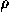 from P to the origin; the angle
from P to the origin; the angle
 (zenith) between the line OP and the positive polar axis; and the
angle
(zenith) between the line OP and the positive polar axis; and the
angle  (azimuth) between the initial ray and the
projection of OP to the equatorial plane. See
Figure 1. As in the case of polar and cylindrical
coordinates,
(azimuth) between the initial ray and the
projection of OP to the equatorial plane. See
Figure 1. As in the case of polar and cylindrical
coordinates,  is only defined up to multiples of
360°, and likewise
is only defined up to multiples of
360°, and likewise  . Usually
. Usually  is assigned a value
between 0 and 180°, but values of
is assigned a value
between 0 and 180°, but values of  between
180° and 360° can also be used; the triples
(
between
180° and 360° can also be used; the triples
(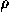 ,
, ,
, ) and
(
) and
(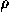 , 360°-
, 360°- , 180°+
, 180°+ ) represent the same
point. Similarly, one can extend
) represent the same
point. Similarly, one can extend 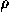 to negative values; the
triples (
to negative values; the
triples (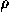 ,
, ,
, ) and
(-
) and
(-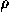 , 180°-
, 180°- , 180°+
, 180°+ ) represent the same
point.
) represent the same
point.
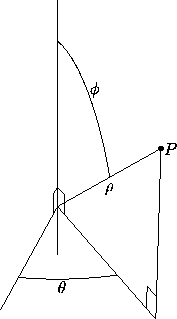
Figure 1: A set of spherical coordinates for P is
(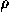 ,
, ,
, )=(10,60°,30°).
)=(10,60°,30°).
Next: 9.4 Relations between Cartesian, Cylindrical, and
Spherical Coordinates
Up: 9 Coordinate Systems in Space
Previous: 9.2 Cylindrical Coordinates in Space
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
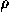 from P to the origin; the angle
from P to the origin; the angle
 (zenith) between the line OP and the positive polar axis; and the
angle
(zenith) between the line OP and the positive polar axis; and the
angle  (azimuth) between the initial ray and the
projection of OP to the equatorial plane. See
Figure 1. As in the case of polar and cylindrical
coordinates,
(azimuth) between the initial ray and the
projection of OP to the equatorial plane. See
Figure 1. As in the case of polar and cylindrical
coordinates,  is only defined up to multiples of
360°, and likewise
is only defined up to multiples of
360°, and likewise  . Usually
. Usually  is assigned a value
between 0 and 180°, but values of
is assigned a value
between 0 and 180°, but values of  between
180° and 360° can also be used; the triples
(
between
180° and 360° can also be used; the triples
(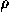 ,
, ,
, ) and
(
) and
(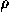 , 360°-
, 360°- , 180°+
, 180°+ ) represent the same
point. Similarly, one can extend
) represent the same
point. Similarly, one can extend 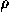 to negative values; the
triples (
to negative values; the
triples (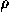 ,
, ,
, ) and
(-
) and
(-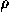 , 180°-
, 180°- , 180°+
, 180°+ ) represent the same
point.
) represent the same
point.

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page