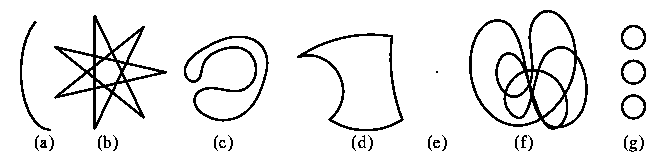

Among the following pictures, which ones show a curve?

We all have an intuitive idea of curves, and we don't generally worry too much about how to define them. But when we start studying curves we see that there are many ways in which we can formalize our intuitive concept. Which is the best?
The answer depends on the context. The important thing is to agree beforehand on which idea we have in mind. Mathematicians usually do this by insisting that their objects of discussion have certain properties (such as ``continuous'' or ``smooth''), in order to make it easier to find out things about the objects -- much as a telemarketer will buy directories of people with certain characteristics, the better to predict their buying patterns.
To state these properties it is convenient to think of a curve as something that you trace with a pen. From the time you put the pen to paper to the time you lift it, there is for each instant a corresponding position of the pen. A correspondence of this kind is called a map, and is represented by a letter, like f. A map goes from one set (here the interval of time during which the curve is being traced) to another (here the plane). For each element of the from-set (a moment of time), the map gives an element of the to-set (a point in the plane). The curve, then, is the set of points touched by the pen at one time or another -- it is the part of the to-set ``reached'' by the map. (So the curve is the image of the map f from the interval [a, b] to R^2. From this point of view, even (e) above is a curve, with f(t) the same for all t.)
We also say that f is a parametrization of the curve, and that the curve is parametrized by an interval of numbers (the from-set).
One objection to this point of view is that the parametrization contains much more information than the curve we see on the page, information that is largely arbitrary: for instance, if we trace around a curve twice as fast we get the same set of points, but the parametrization is different. This way to store extra information will actually turn out to be advantageous, but in any case I emphasize that the parametric point of view is only one possible way to formalize our intuitive idea of curves. The important thing is to have the intuitive idea clear.
We will always want our curves to be continuous; this means the pen doesn't jump from one position to another instantaneously. (Of course a real pen could not do this anyway, but our idealized pen is not subject to such pedestrian limitations.) (So ``continuous'' properly refers to the parametrization, but we'll use it for the parametrized curve as well. We will do the same thing with other properties.)
 Which among the curves (a)--(g) above are continuous?
Which among the curves (a)--(g) above are continuous?
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: Jul 10, 1995 ---
Last modified: Fri Jun 14 10:31:43 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.